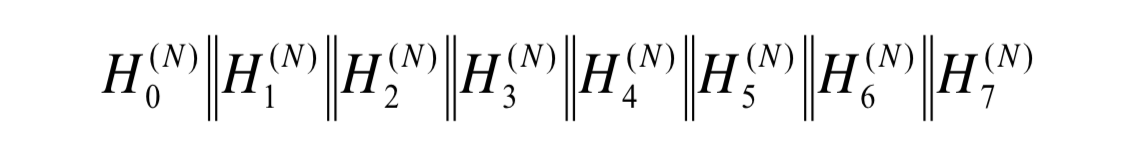简介
安全散列算法(英语:Secure Hash Algorithm,缩写为SHA)是一个密码散列函数家族,是FIPS所认证的安全散列算法。能计算出一个数字消息所对应到的,长度固定的字符串(又称消息摘要)的算法。且若输入的消息不同,它们对应到不同字符串的机率很高。
SHA家族的五个算法,分别是SHA-1、SHA-224、SHA-256、SHA-384,和SHA-512,由美国国家安全局(NSA)所设计,并由美国国家标准与技术研究院(NIST)发布;是美国的政府标准。后四者有时并称为SHA-2。SHA-1在许多安全协定中广为使用,包括TLS和SSL、PGP、SSH、S/MIME和IPsec,曾被视为是MD5(更早之前被广为使用的杂凑函数)的后继者。但SHA-1的安全性如今被密码学家严重质疑;虽然至今尚未出现对SHA-2有效的攻击,它的算法跟SHA-1基本上仍然相似;因此有些人开始发展其他替代的杂凑算法。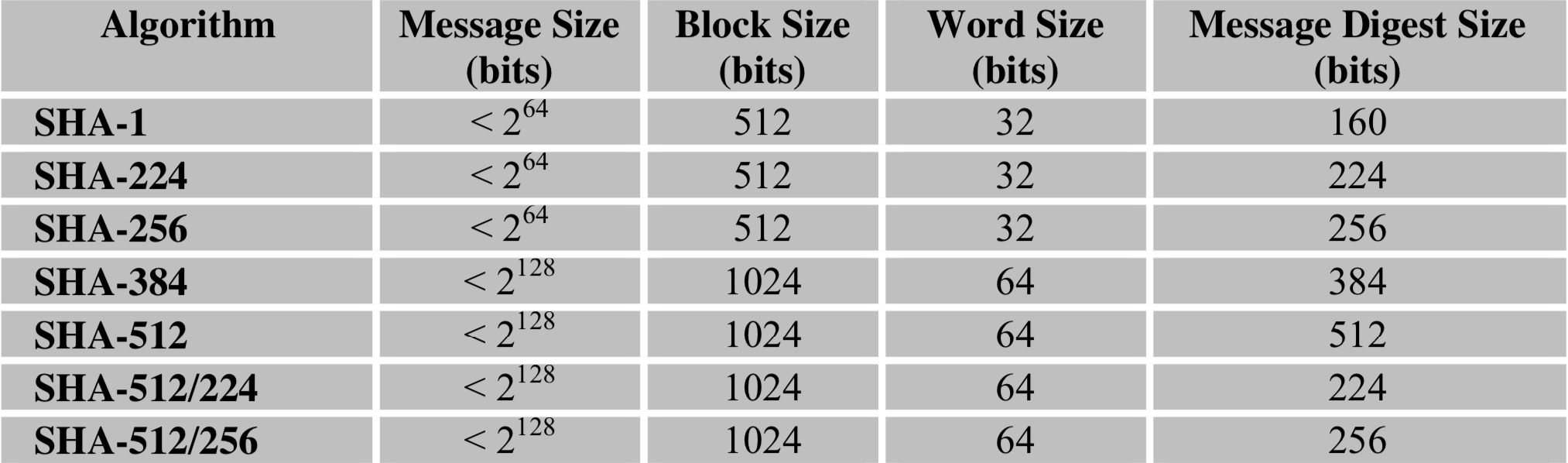
下面以SHA-256算法为例
定义
术语表
比特:一个二进制的数字,值为0或1。
字节:长度为8个比特的数字。
字:长度为32比特的数字。
参数表
$a,b,c,…,h$ “字”在计算哈希值过程中的操作变量。
$H^{(i)}$ 第i个哈希值,是初始值,是用来决定信息摘要的最终值。
$H^{(i)}_j$ 第i个哈希值的第j个“字”。$H^{(i)}_0$表示哈希值i最左侧的“字”。
$K_t$ 哈希计算第t次迭代使用的常量。
$M$ 用来执行哈希算法的信息。
$M^{(i)}$ 第i个信息块,长度为512比特。
$M^{(i)}_j$ 第i个信息块的第j个“字”,$M^{(0)}_j$表示信息块i最左侧的“字”。
$T$ 哈希计算过程中的临时使用“字”。
$W_t$ 信息表中的第t个“字”。
操作符
$\wedge$ 按位逻辑与运算。
$\vee$ 按位逻辑或运算。
$\oplus$ 按位逻辑异或运算。
$+$ 加法运算之后再$ mod 2^{32}$。
$¬$ 按位逻辑非运算。
$\ll$ 按位左移运算。
$\gg$ 按位右移运算。
$ROTR^n(x)$ x表示“字”, 0 < n < 32,$ROTR^n(x)=(x\gg n) \vee (x\ll 32-n)$。
$SHR^n(x)$ x表示“字”, 0 < n < 32,$SHR^n(x)=x \gg n$。
函数和常量
函数
$Ch(x,y,z)=(x∧y)⊕(¬x∧z)$
$Maj(x,y,z)=(x∧y)⊕(x∧z)⊕(y∧z)$
$∑^{\{256\}}_0(x)=ROTR^2(x)⊕ROTR^{13}(x)⊕ROTR^{22}(x)$
$∑^{\{256\}}_1(x)=ROTR^6(x)⊕ROTR^{11}(x)⊕ROTR^{25}(x)$
$σ^{\{256\}}_0(x)=ROTR^7(x)⊕ROTR^{18}(x)⊕SHR^{3}(x)$
$σ^{\{256\}}_1(x)=ROTR^{17}(x)⊕ROTR^{19}(x)⊕SHR^{10}(x)$
常量
算法需要用到64个“字”常量$K^{\{256\}}_0,K^{\{256\}}_1,…,K^{\{256\}}_{63}$,这些“字”是截取前64个质数的立方根小数部分的前32个比特位得到的。已十六进制的形式从左到右如下:
预处理
填充信息
假设有一段信息M,长度为l。在信息的末尾拼接一个比特“1”,接着添加k个比特“0”,k是方程$l+1+k≡448 mod 512$的最小非负解。然后拼接一个64比特的二进制数表示M的长度l。举例,新“abc”(ASCII占八个比特)长度为3 * 8 = 24,k = 448 - 1 - 24 = 423,整个信息的长度变为512比特的倍数。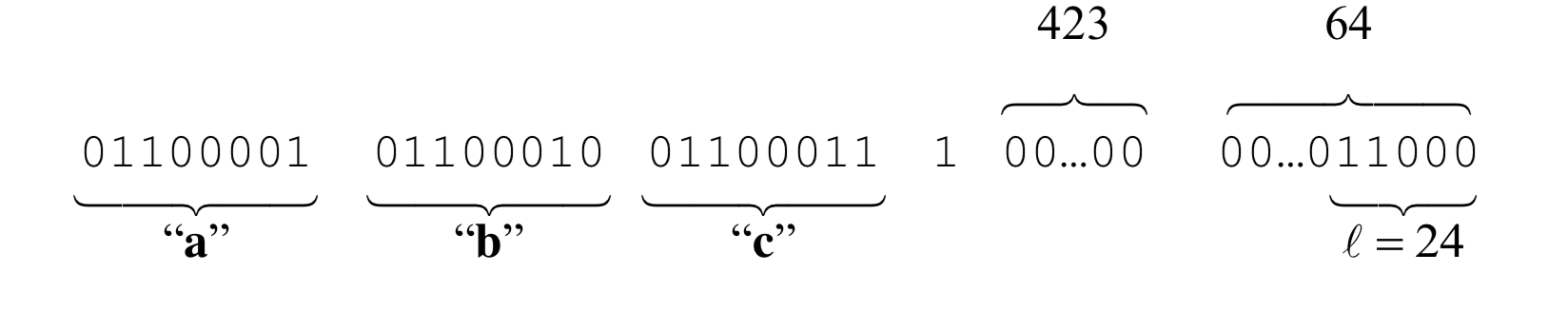
现在信息可以划分N个512比特的信息块$M^{(1)},M^{(2)},…,M^{(N)}$,因为512比特的信息块又可以表示为16个32比特的“字”,第i个信息块的第一个“字”$M^{(i)}_{0}$,下一个是$M^{(i)}_{1}$,以此类推直到$M^{(i)}_{15}$。
设置初始哈希值
最终的信息摘要长度是256比特,每个哈希值是一个32比特的“字”,所以这里需要8个初始哈希值。
这些“字”是截取前8个质数的平方根小数部分的前32个比特位得到的。
算法
SHA-256算法需要用到信息M,长度为l,$0<l<2^{64}$、信息表(有64个“字”,通过扩展$M^{(i)}$得到,前16个“字”直接使用$M^{(i)}$,往后的“字”通过计算获取(具体情况看伪代码步骤1. Prepare the message schedule)$W_0,W_1,…,W_{63}$、八个操作变量$a, b, c, …, h$(这些变量用来完成从$H^{(0)}$到$H^{(N)}$的映射)、计算过程得到哈希值$H^{(i)}_0,H^{(i)}_1,…,H^{(i)}_{7}$(初始值为$H^{(0)}$,在每个信息块计算结束时更新,直到计算出$H^{(N)}$)、两个临时“字”变量$T_1,T_2$。
PS:以下过程中+运算之后都需要$ mod 2^{32}$。
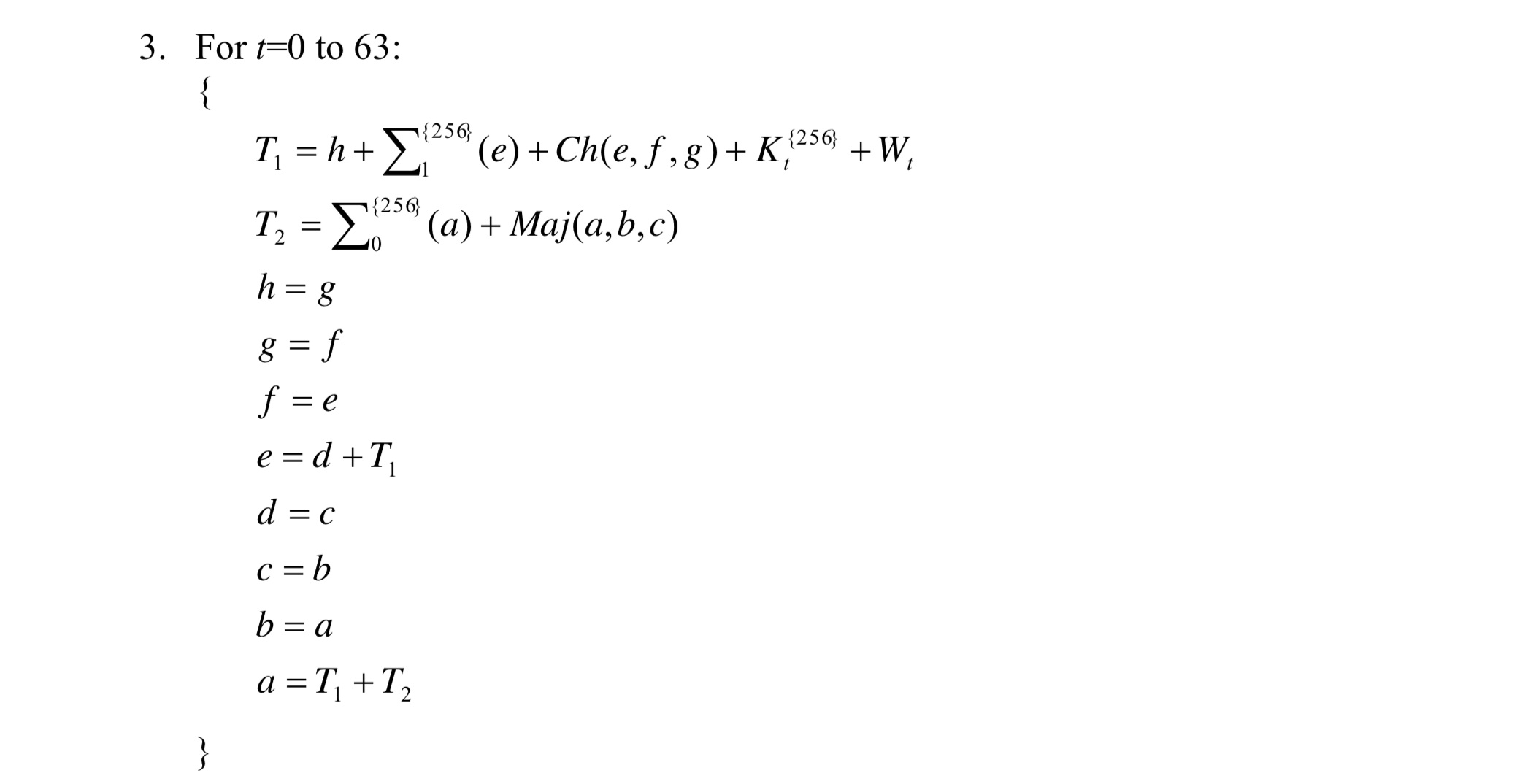

经过N次信息块的计算之后,最后再把所有的$H^{(N)}$拼接起来之后得到信息摘要。