博弈论简介
博弈论,又称为对策论(Game Theory)、赛局理论等,既是现代数学的一个新分支,也是运筹学的一个重要学科。
博弈论主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。 博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。生物学家使用博弈理论来理解和预测进化论的某些结果。
博弈论已经成为经济学的标准分析工具之一。在金融学、证券学、生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。
巴什博弈
一个简单的游戏
定义一个取石子的游戏规则如下:
(1)有两个玩家,分别记作玩家 I 和玩家 II。
(2)有21个石子放在桌子上。
(3)每个玩家一次可以取走1或2或3个石子。
(4)两个玩家交替进行取石子操作,由玩家 I 开始游戏。
(5)取走最后一个石子的玩家获胜(如果玩家没有石子可取,他就输了)。
玩家怎么做才能获胜?使用向后归纳法来分析玩家当前状态是输是赢。
如果玩家面临0个石子,那么他就输了。
如果玩家面临1、2、3个石子,那么他就赢了。
如果玩家面临4个石子,那么他就输了(因为他一次取不完,而剩下的石子下一个玩家可以一次取完)。
如果玩家面临5、6、7个石子,那么他就赢了(因为他可以留下4个石子,下一个玩家必输)。
…
必胜点和必败点
假如使用N来表示必胜点,P来表示必败点。有如下规定:
(1)游戏的终结点使用P表示。
(2)对于每一个N点,至少可以有一种操作可以进入P点。
(3)对于每一个P点,每一种操作都只能进入N点。
假如把上面取子的规则改成{1,3,4},会出现什么情况呢?
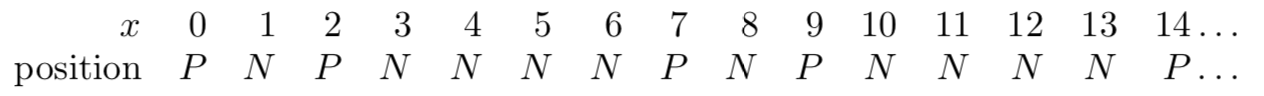
整个序列一直在重复PNPNNNN这个模式。如果有100个石子,当前位置是必胜还是必败?
100 mod 7 = 2,整个模式只有 0 和 2 是必败点,所以100应该是一个必败点。
尼姆博弈
假如把游戏规则改一下,现在有三堆石子,每次只能操作一堆石子,可以从中拿走任意数量。这个游戏该怎么确定胜败规律呢?
预备分析
首先可以确定的就是(0, 0, 0)作为终结点标记为P,如果是只剩下一堆的情况(0, 0, x),x > 0,那么这是一个N点。如果剩下两堆,并且这两堆数目相同,很明显这是一个P点(比如(0, 1, 1)和(0, 2, 2),当前玩家从一堆中拿多少个,下一个玩家就从另一堆中拿多少个)。如果剩下数目不同的两堆,那么这是一个N点。
如果三堆都还有石子呢?像(1, 1, 1)、(1, 1, 2)、(1, 1, 3)和(1, 2, 2)这些点明显是N点(它们可以被当前玩家操作成(0, 1,1)或者(0, 2, 2))。接下来看一下(1, 2, 3),这是一个P点,因为不管怎么操作它都会进入之前所发现的N点中。也许我们可以继续分析找出接下来的P点(1, 4, 5)、(2, 4, 6),但是这样分析下去是很困难的。
如果继续分析下去,你们可能会发现这里也存在一种模式。
尼姆和
我们知道所有的非负整数都可以表达为二进制。
$x=x_m2^m+x_{m-1}2^{m-1}+…+x_12+x_0$
我们可以使用$(x_mx_{m-1}…x_1x_0)_2$来表示一个非负整数的二进制形式,比如$22=(10110)_2$。
定义:$(x_m…x_0)_2$和$(y_m…y_0)_2$的尼姆和可以写作$(x_m…x_0)_2⊕(y_m…y_0)_2=(z_m…z_0)_2$,对于所有的k,有$z_k=x_k+y_k (mod 2)$。
比如求一下22和51的尼姆和:
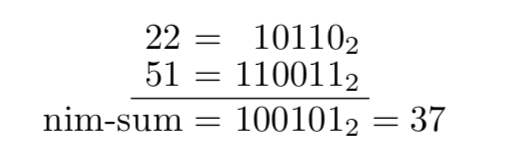
⊕就是我们熟知的异或运算,它满足以下规律:
$x⊕(y⊕z)=(x⊕y)⊕z$
$x⊕y=y⊕x$
$0⊕x=x$
$x⊕x=0$
如果 $x⊕y=x⊕z$ ,就表示y=z。
定理1:在尼姆游戏的规则下,如果$(x_1,x_2,x_3)$是一个P点,当且仅当$x_1⊕x_2⊕x_3=0$。(这个定理适用于多堆石子游戏,不仅仅只对3堆有效)
证明:
假设我们用集合X来表示尼姆和为0的点,集合Y表示其他的点。接下来我们检验一下必胜点和必败点的定义:
(1)终结点都在集合X中,终结点的定义就是任何一堆都没有石子,那么$0⊕0⊕0…. = 0$。
(2)对于所有集合Y中的点,都可以通过至少一种操作进入X。假设我们找到Y中一个点,按照二进制的形式纵向排列每一堆石子的个数(像尼姆和定义下面的举例一样),尼姆和不为0,一定是某些二进位上存在奇数个’1’,找到最左边出现奇数个’1’的一列,选取这一列有’1’的一堆进行操作,让每个二进制位的纵向排列都是偶数个’1’。
(3)对于集合X中的点,每一个操作都会进入Y。如果$(x_1,x_2,…)$是集合X中的点,如果我们将$x_1$变成$x_1^{‘}<x_1$,那么我们不能证明,因为如果这个等式成立,就表示$x_1=x_1^{‘}$(不存在一个都不取得操作)。所以$x_1^{‘}⊕x_2…≠0$,这就表示$(x_1^{‘},x_2…)$不在集合X中。
以上过程说明X中的点都是P点。
证毕。
有向图博弈
所有的取子游戏,其实都可以使用一个有向图来表示。而且接下来会讲到Sprague-Grundy函数(简称SG函数),这个函数可以理解为PN原理的升级版,而且函数的结果也不仅仅只包含P点和N点的信息。
有向图
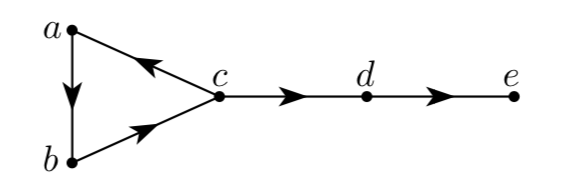
定义:一个有向图G,由一对(X, F)组成,X是一个非空点(位置)集合,F是一个函数,x 是X的元素,F(x)表示当前点 x 可能到达的后继点,F(x) ⊂ X。如果F(x)是空集,那么 x 就是终结点。
举个例子,本文第一个取子游戏可表示为(X, F),X = {0, 1, … , n},F = {k-3, k-2, k-1}(小于0的元素忽略),对于x点可以到达的点有:F(0) = ∅,F(1) = {0},F(2) = {0, 1} … 。

Sprague-Grundy函数
有向图博弈可以通过PN原理来分析,而且也可以通过SG函数来分析。
定义:一个有向图(X, F)的SG函数,在有向图定义的基础上,取值是非负整数有如下公式。
$g(x)=min \{n≥0: n≠g(y) , y∈F(x)\}$
换句话来说,g(x)是不在x的后继点的SG函数值中的非负整数。
接下来分析本文第一个取子游戏的SG函数,终结点0,没有后继点,g(0) = 0;点1可以到达点0,g(1) = 1;点2可以到达点1、0,g(2) = 2;点3可以到达点2、1、0,g(3) = 3;点4可以到达点3、2、1,g(4) = 0。接着分析下去:
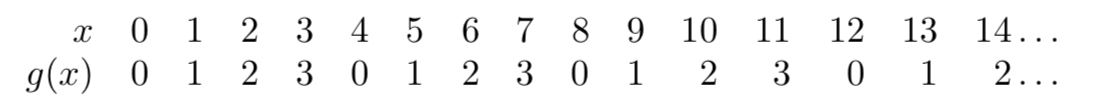
有没有发现SG函数与PN原理的相似之处?
(1)终结点的g(x) = 0。
(2)如果在点x处g(x) ≠ 0,那么x的后继点至少存在一个g(y) = 0。
(3)如果在点x处g(x) = 0, 那么所有x的后继点,g(y) ≠ 0。
注意:这里的有向图存在SG函数不允许图中存在有环的情况,而且途中所有路径必须是有限的(递进有限的有向图)。
多个合作博弈组合
如果把多个合作游戏放在一起,玩家轮流操作,每次只能在一个合作游戏中按规则操作一次,如何预测玩家的胜负呢?这里就需要用上面提到的SG函数来解决了。
合作博弈的和
假设我们有n个递进有限的有向图$G_1=(X_1,F_1),G_2=(X_2,F_2),…,G_n=(X_n,F_n)$,它们可以组合成一个新的有向图$G=(X,F)$,它叫作$G_1,G_2,…G_n$的和,记作$G=G_1+G_2…+G_n$。集合 X 是一个笛卡尔积,$X=X_1×X_2…×X_n$,其中的元素是n个点的元组$(x_1,x_2,…,x_n)$,对于所有的$x_i∈X_i$,元素$x=(x_1,x_2,…,x_n)∈X$。F(x)存在如下等式:
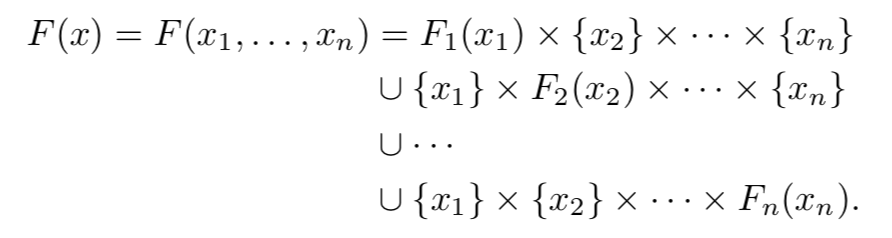
对于点中$x=(x_1,x_2,…,x_n)$,任意一个点$x_i$都可以找到它的后继点集合$F_i(x_i)$,并且x的后继点都可以在上图函数F中找到,所以 G 是有向图$G_1,…G_n$的和。
如果$G_i$是递进有限的,那么 G 也是递进有限的。因为点$x=(x_1,x_2,…,x_n)$的后继点的个数是所有组合有向图$x_i$的后继点个数的和。
尼姆博弈就可以看做三个巴什博弈的和,虽然一堆石子玩起来很简单,但是多个博弈组合起来玩也许就会很复杂了。
Sprague-Grundy定理
显然这个定理一定包含了SG函数,还会用到尼姆和。而且这个定理也可以起到PN原理的作用(判断当前点的胜败情况),证明过程与定理1类似。
定理2:如果$g_i$表示递进有限的有向图$G_i$的SG函数,i = 1, … , n,那么$G=G_1+G_2…+G_n$存在SG函数$g(x_1,…,x_n)=g_1(x_1)⊕g_2(x_2)…⊕g_2(x_n)$。
证明:
假设$x=(x_1,x_2,…,x_n)$是集合X中的一点,那么存在$b=g(x_1)⊕…⊕g(x_n)$。
那么证明以下两点 g 满足SG函数的定义:
(1)对于每一个非负整数 a < b, 存在 x 的后继点 y,g(y) = a。
(2)在 x 的所有后继点中,不存在 g(y) = b。
为了证明(1),假设 d = a ⊕ b,在二进制展开d中找到最左边出现‘1’的二进位k(从右向左数),因为b > a,所以 b 在第 k 位一定是’1’,又因为$b=g(x_1)⊕…⊕g(x_n)$,那么一定存在一个$g_i(x_i)$使得 b 在第 k 位是奇数个’1’,假设i = 1,那么$d⊕g_1(x_1) < g_1(x_1)$,所以存在一种操作$g_1(x_1^{‘})=d⊕g_1(x_1)$,$(x_1,x_2,…,x_n)$可以通过符合规则的操作达到$(x_1^{‘},x_2,…,x_n)$。
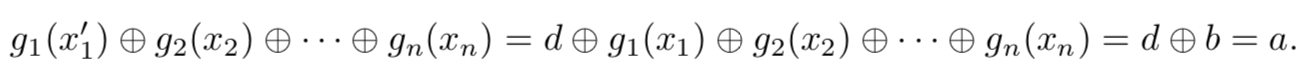
最后证明(2)就比较简单了,假设$(x_1,x_2,…,x_n)$的后继点是$(x_1^{‘},x_2,…,x_n)$,如果$g_1(x_1)⊕g_2(x_2)…⊕g_n(x_n)=g_1(x_1^{‘})⊕g_2(x_2)…⊕g_n(x_n)$,那么$g_1(x_1)=g_1(x_1^{‘})$,因为$x_1^{‘}$是$x_1$的后继点,根据SG函数的定义显然$g_1(x_1)≠g_1(x_1^{‘})$。
证毕。
现在我们可以利用SG定理来分析多个合作博弈组合的胜负规律了。
参考文档
《GAME THEORY》 by Thomas S. Ferguson