计算几何之凸包

简介

　　凸包（Convex Hull）是一个计算几何（图形学）中的概念。
　　在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1，…Xn)的凸组合来构造.
　　在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。
　　用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。

　　

线段属性

三个问题：
1.已知两个有向线段$\mathop{p_0p_1}\limits^{→}$和$\mathop{p_0p_2}\limits^{→}$，如何判断关于点$p_0$从$\mathop{p_0p_2}\limits^{→}$到$\mathop{p_0p_1}\limits^{→}$的方向是顺时针还是逆时针？
2.已知两个有向线段$\mathop{p_0p_1}\limits^{→}$和$\mathop{p_1p_2}\limits^{→}$，如果我们从$\mathop{p_0p_1}\limits^{→}$经过$\mathop{p_1p_2}\limits^{→}$，在点$p_1$处需要左转还是右转？
3.怎么确定两个有向线段$\mathop{p_0p_1}\limits^{→}$和$\mathop{p_3p_4}\limits^{→}$是否相交？
以上都是在确定两个向量的关系，为了解决问题需要理解何为交叉积。
两个向量的交叉积计算可以用一个矩阵行列式来表达：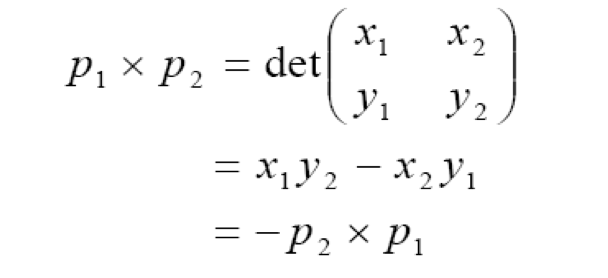

也可以理解为一个有正负的平行四边形面积。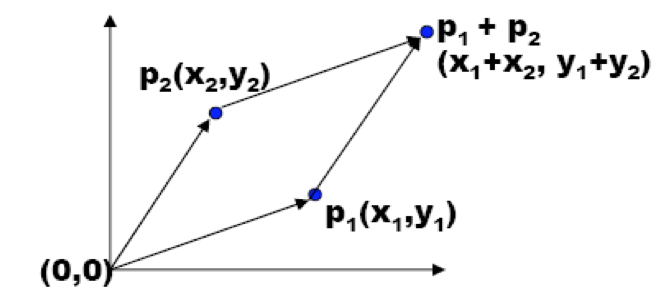

对于$p_1×p_2$的计算结果：
大于0 : 关于点(0, 0)，p2到p1的方向是顺时针
小于0 : 逆时针
等于0 : 共线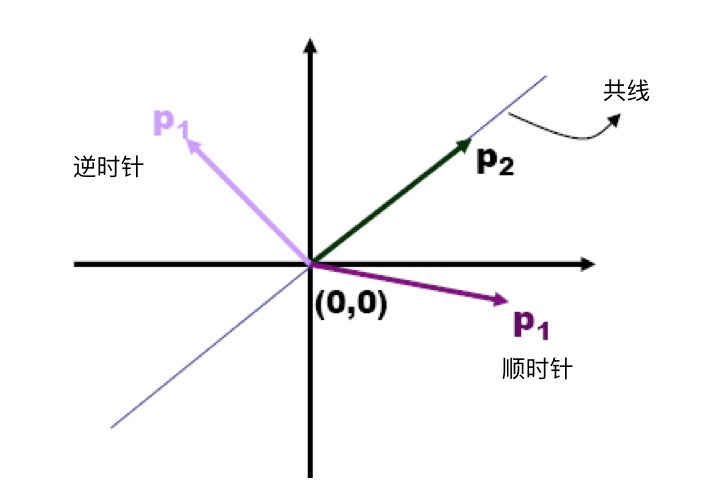

问题1

已知三个点的坐标为$p_0(x_0, y_0),p_1(x_1, y_1),p_2(x_2, y_2)$。
p0作为起点，计算交叉积：
$\mathop{p_0p_1}\limits^{→}=p_1-p_0=(x_1-x_0,y_1-y_0)$
$\mathop{p_0p_2}\limits^{→}=p_2-p_0=(x_2-x_0,y_2-y_0)$
$\mathop{p_0p_1}\limits^{→}×\mathop{p_0p_2}\limits^{→}=(x_1-x_0)(y_2-y_0)-(x_2-x_0)(y_1-y_0)$
大于0 : 顺时针
小于0 : 逆时针
等于0 : 共线

问题2

通过交叉积可以直接判断。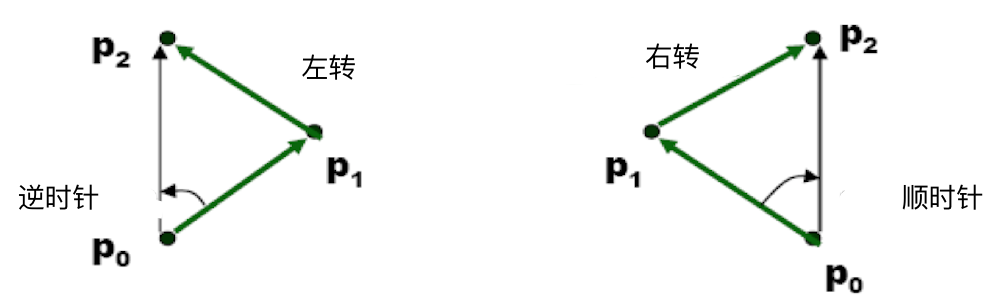

计算$(p_2-p_0)×(p_1-p_0)$
大于0 : 右转
小于0 : 左转
等于0 : 共线

问题3

线段相交可分为两种情况，一种是交点出现在线段中，一种交点出现在端点。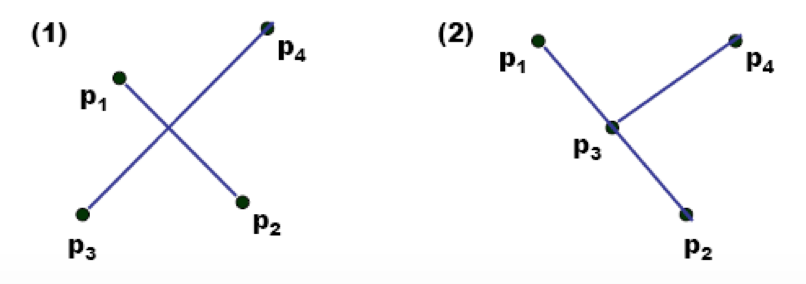

第二种情况比较特殊，需要针对每个点进行判断，直接看一下伪代码：

//p表示点坐标，该函数求向量p_kp_j到p_kp_i的方向。
DIRECTION(p_i,p_j,p_k)
{	
	return (p_i - p_k) × (p_j - p_k)	//求交叉积
}
//这个函数要结合DIRECTION一起来判断共线
ON-SEGMENT(p_i,p_j,p_k)
{
	if min(x_i, x_j) <= x_k <= max(x_i, x_j) and min(y_i, y_j) <= y_k <= max(y_i, y_j)
    	return true
    else
    	return false
}
//判断两个线段是否相交
SEGMENTS-INTERSECT(p_1,p_2,p_3,p_4)
{
	d1 = DIRECTION(p_3,p_4,p_1)
    d2 = DIRECTION(p_3,p_4,p_2)
    d3 = DIRECTION(p_1,p_2,p_3)
    d4 = DIRECTION(p_1,p_2,p_4)
    if((d1>0 and d2<0) or (d1<0 and d2>0)) and ((d3>0 and d4<0) or (d3<0 and d4>0))
    	return true
    else if d1 = 0 and ON-SEGMENT(p_3,p_4,p_1)
    	return true
    else if d2 = 0 and ON-SEGMENT(p_3,p_4,p_2)
    	return true
    else if d3 = 0 and ON-SEGMENT(p_1,p_2,p_3)
    	return true
    else if d4 = 0 and ON-SEGMENT(p_1,p_2,p_4)
    	return true
    else 
    	return false
}

Graham-Scan算法

算法步骤：
集合Q中有m个点，找出y坐标最小的点$p_0$。
Q剩下的点按照关于$p_0$的极角大小逆时针排序得到$p_1…p_m$。
创建栈S来存储凸包的顶点，Push($p_0$,S)，Push($p_1$,S)，Push($p_2$,S)。
按顺序遍历剩下的点->
for i = 3…m
while(关于Top(S)的前一个点，经过Top(S)到$p_i$的转动方向非左转）
Pop(S)
Push($p_i$,S)
return S
整个算法的大致过程如下图所示：

模板代码

以前在kuangbin大神的博客学习过，所以我就直接粘贴他的模板了。

#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<iostream>
using namespace std;
const int MAXN=1000;

struct point
{
    int x,y;
};
point list[MAXN];
int stack[MAXN],top;

int cross(point p0,point p1,point p2) //计算叉积  p0p1 X p0p2 
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);
}    
double dis(point p1,point p2)  //计算 p1p2的 距离 
{
    return sqrt((double)(p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y));
}    
bool cmp(point p1,point p2) //极角排序函数 ， 角度相同则距离小的在前面 
{
    int tmp=cross(list[0],p1,p2);
    if(tmp>0) return true;
    else if(tmp==0&&dis(list[0],p1)<dis(list[0],p2)) return true;
    else return false;
}    
void init(int n) //输入，并把  最左下方的点放在 list[0]  。并且进行极角排序 
{
    int i,k;
    point p0;
    scanf("%d%d",&list[0].x,&list[0].y);
    p0.x=list[0].x;
    p0.y=list[0].y;
    k=0;
    for(i=1;i<n;i++)
    {
        scanf("%d%d",&list[i].x,&list[i].y);
        if( (p0.y>list[i].y) || ((p0.y==list[i].y)&&(p0.x>list[i].x)) )
        {
            p0.x=list[i].x;
            p0.y=list[i].y;
            k=i;
        }    
    }    
    list[k]=list[0];
    list[0]=p0;
    
    sort(list+1,list+n,cmp);
}     

void graham(int n)
{
    int i;
    if(n==1) {top=0;stack[0]=0;}
    if(n==2)
    {
        top=1;
        stack[0]=0;
        stack[1]=1;
    }    
    if(n>2)
    {
        for(i=0;i<=1;i++) stack[i]=i;
        top=1;
        
        for(i=2;i<n;i++)
        {
            while(top>0&&cross(list[stack[top-1]],list[stack[top]],list[i])<=0) top--;
            top++;
            stack[top]=i;
        }    
    }    
}

int main(int argc, const char * argv[]) {
    // insert code here...
    int n;
    scanf("%d", &n);
    init(n)
    graham(n);
    /*
     stack数组中存储了凸包的顶点
     */
    return 0;
}

Jarvis-March算法

算法思想：
集合Q中有m个点，找出x和y坐标最小的点$p_0$作为当前凸包顶点k。
do {
for 非k的其余顶点
找到一个顶点s，使得集合Q中点都在ks线段的左侧
记录顶点s作为凸包的顶点
k=s
} while (k != $p_0$)
整个算法的大致过程如下图所示：

上图提供了一个算法的简略过程，关键步骤还是怎么确定所有集合点在线段的左侧。

模板代码

#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<iostream>
using namespace std;
const int MAXN=1000;

struct point
{
    int x,y;
    bool extreme;
};

point list[MAXN];

bool ToLeft(point p, point q, point s)
{
    int area2 =   p.x * q.y - p.y * q.x
    + q.x * s.y - q.y * s.x
    + s.x * p.y - s.y * p.x;
    return area2 > 0;    //左侧为真
}

int ltl(int n)
{
    int LTL = 0;
    for (int k = 1; k < n; k++)
        if (list[k].y < list[LTL].y ||
            (list[k].y == list[LTL].y &&
             list[k].x < list[LTL].x))
            LTL = k;
    return LTL;
}

void jarvis(int n)
{
    for (int k = 0; k < n; k++)
        list[k].extreme = false;    //首先将所有点标记为非极点
    
    int LTL = ltl(n);    //找到LTL
    int k = LTL;            //将LTL作为第一个极点
    
    do
    {
        list[k].extreme = true;    //判定为极点
        int s = -1;
        
        //选取下一个极点，每次比较两个点s和t，
        //做点t和有向边ks的to left test，最终找到s
        for (int t = 0; t < n; t++)
            if (t != k && (s == -1 || !ToLeft(list[k], list[s], list[t])))
                s = t;    //如果t在s右边
        k = s;    //s变为下一次查找的起点
    } while (LTL != k);
}

int main(int argc, const char * argv[]) {
    // insert code here...
    int n;
    scanf("%d", &n);
    for(int i=0;i<n;i++)
    {
        scanf("%d%d",&list[i].x,&list[i].y);
    }
    jarvis(n);
    /*
     list表中的结点extreme为true的就是凸包的顶点
     */
    return 0;
}