二分图最大匹配

Posted on | | Visitors:

二分图

　　二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

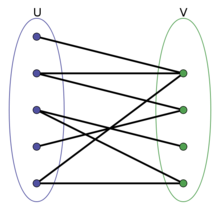
　　image
　　切记二分图中不存在顶点数为奇数的环路，通常可以使用染色法（该方法使用两种颜色，相邻的点标记不同的颜色）来辨别二分图。

匹配

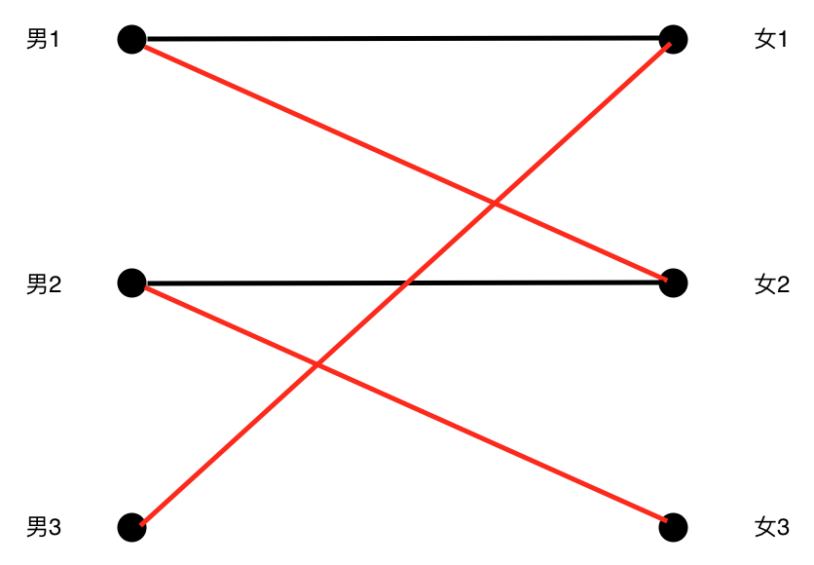
　　二分图的“匹配”是指一些边的集合，并且任意两条边没有公共点。下图中红色标注的即为匹配边。
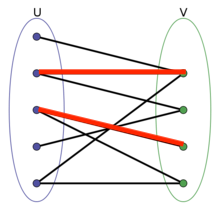
　　image

最大匹配

　　二分图的“最大匹配”，指的是二分图的所有匹配中边数最多的匹配。

交替路

　　从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边……形成的路径叫交替路。

增广路

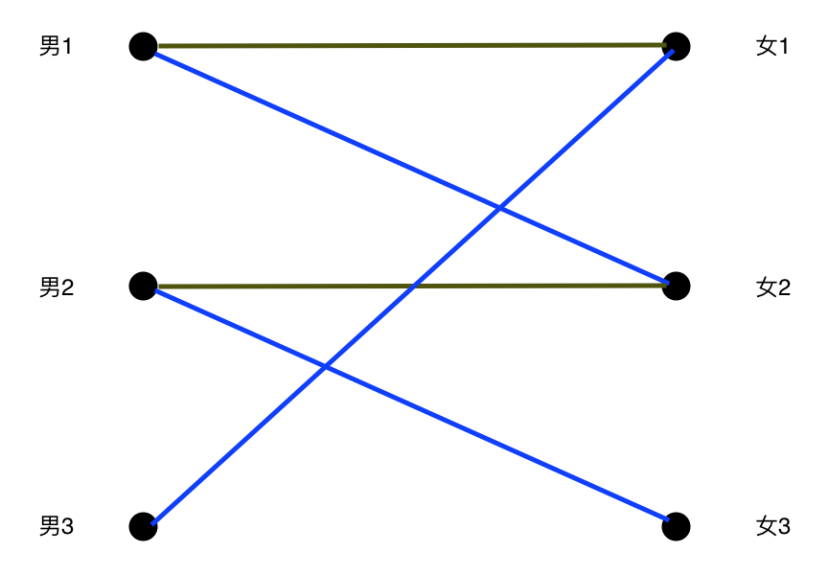
　　从一个未匹配点出发，走交替路到达另一个未匹配点，并且非匹配边比匹配边多一条，那么这条路径叫增广路。如果用增广路中的非匹配边代替原来的匹配边，可以使匹配数量增加一个。下图中蓝色和红色标注表示当前匹配的一条增广路。
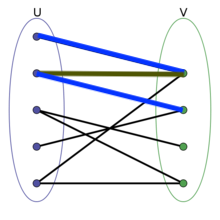
　　image
　　定理：一个匹配是最大匹配当且仅当它不存在增广路。

匈牙利算法

　　匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。美国数学家哈罗德·库恩于1955年提出该算法。此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Dénes Kőnig和Jenő Egerváry的工作之上创建起来的。
　　若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边（即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。
　　算法轮廓：
　　（1）置M为空
　　（2）找出一条增广路径P，通过异或操作获得更大的匹配M’代替M
　　（3）重复（2）操作直到找不出增广路径为止

举例说明

　　假如一个班上有3个男生和3个女生，每个男生都有喜欢的女生（可以有多个），每个男生只会和自己喜欢的女生谈恋爱，怎么撮合最多的情侣关系？
　　男1喜欢女1和女2，男2喜欢女2和女3，男3只喜欢女1。
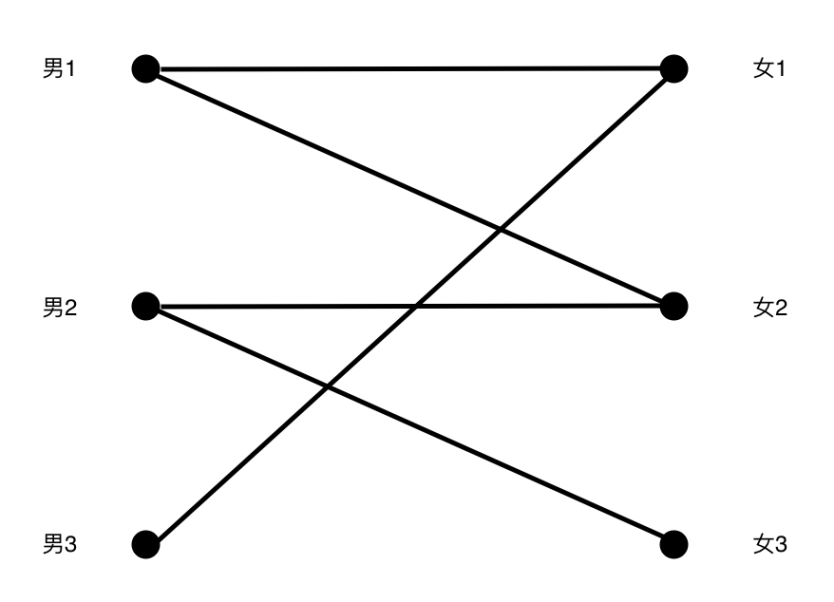
　　image
　　从男1开始配对，没啥难度，直接找到（男1，女1）。
　　PS：单独的一条非匹配边也可以叫做增广路。
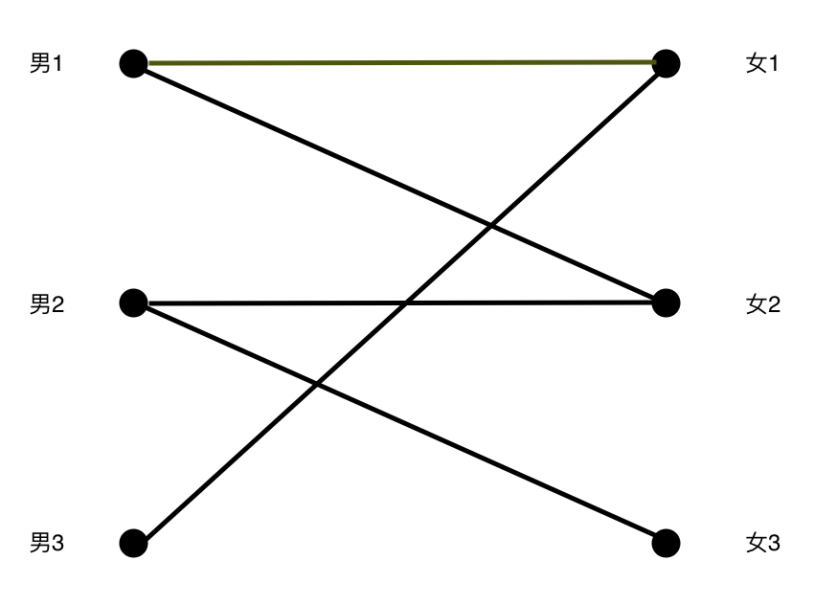
　　image
　　接下来看男2，也没啥问题，找到（男2，女2）。
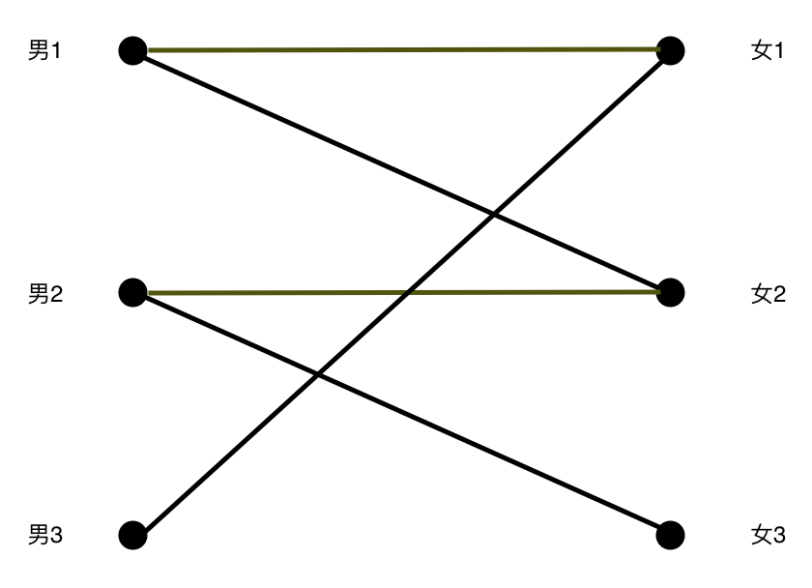
　　image
　　好了，轮到男3，但是他唯一的心动女生已经被选了。。。
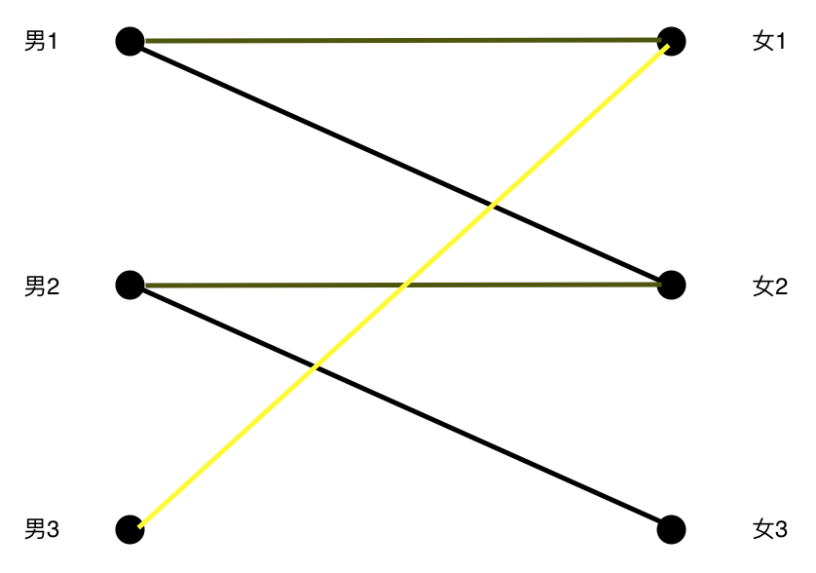
　　image
　　我们知道女1是和男1配对了，那么男1可以换一个妹子吗？
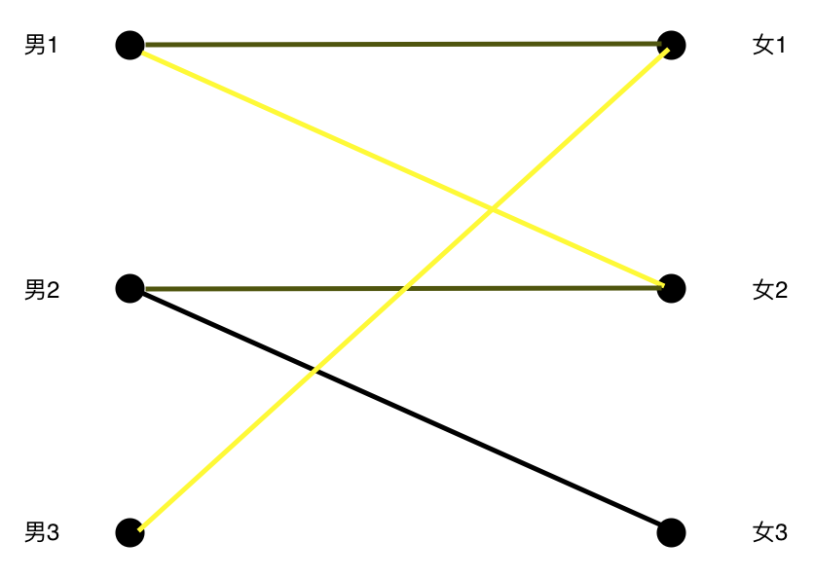
　　image
　　男1准备换女2的时候又发现女2也有主了，那么男2可以换一个妹子吗？
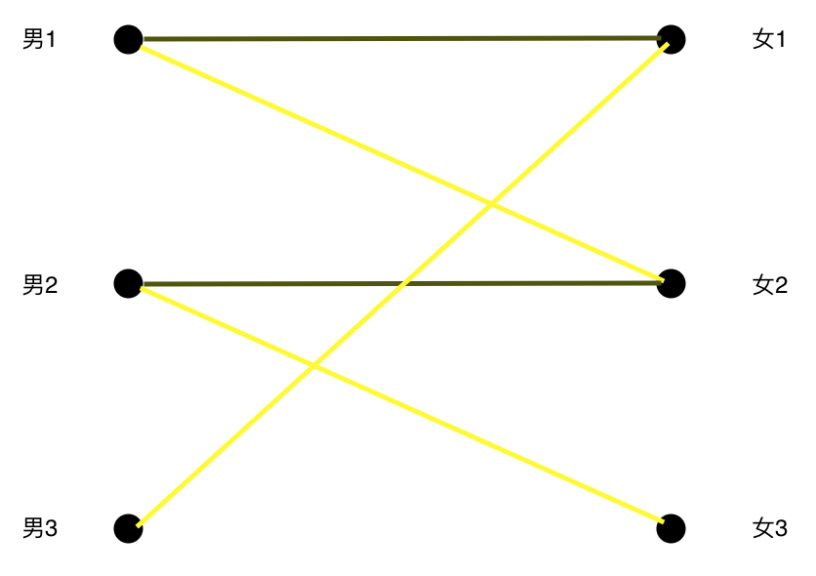
　　image
　　嘿嘿，原来女3这个妹子还没人选。
　　image
　　以上标黄线的图就是寻找增广路的过程，接着让非匹配边替换匹配边得到新的匹配集合。
　　image

模板代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <stdio.h>
#include <string.h>

int g[105][105],used[105],linker[105];
//g用来记录二分图左集合到右集合的关系边
//在每次寻找增广路的过程中used用来标记不能修改匹配的右集合点
//linker从右集合指向左集合反向记录匹配
int uN,uM; //二分图左右集合点数量

int dfs(int n) {
    int m;
    for (m = 0; m < uM; m++) {
        //当前两个点存在关系边，并且m点还没有尝试过修改匹配。
        if (g[n][m] && !used[m]) {
            used[m] = 1;
            //如果m点没有匹配或者m点可以修改匹配，那么就找到了一条增广路。
            if (linker[m] == -1 || dfs(linker[m])) {
                linker[m] = n;
                return 1;
            }
        }
    }
    return 0;
}

int hungary() {
    int res = 0;
    int n;
    memset(linker, -1, sizeof(linker));
   	//依次为左集合的点寻找增广路
    for (n = 0; n < uN; n++) {
        //每次找增广路要重置标记数组
        memset(used, 0, sizeof(used));
        if (dfs(n)) {
            res++;
        }
    }
    return res;
}

int main(int argc, const char * argv[]) {
    int n, m, k;	//n和m是临时变量，k表示关系边的数量
    memset(g, 0, sizeof(g));
    scanf("%d%d%d", &uN, &uM, &k);
    //录入关系边
    while (k--) {
        scanf("%d%d", &n, &m);
        g[n][m] = 1;
    }
    printf("%d\n",hungary());
    return 0;
}

Hopcroft-Karp算法

　　HK算法的作用也是求二分图最大匹配，它在匈牙利算法的基础上做了一些改进，并且提升了效率。假设二分图的结点数量是n，匈牙利算法的时间复杂度为O(n^3)，HK算法的时间复杂度为O(n^2.5)。

推导理论

　　本来如果只有原版英文资料我会做一些翻译，但是我找到了完整的中文版论文。
　　A n^2.5 algorithm for maximum matchings in bipartite graphs-[中文版, John E. Hopcroft & Richard M. Karp].pdf
　　其实看完整片论文我们只需要一个关键性的结论。
　　假设P是我们我们要找的增广路径，M表示匹配集合，s是我们所求的最大匹配基数（匹配对数）。
　　注意M0表示空集，P0表示M0的增广路径，|P|表示增广路径的长度，通过s次寻找增广路径就能找到最大匹配。有以下序列：
　　$|P_0|,|P_1|…|P_s|$
　　在这个序列中最多只有$2⎣ \sqrt{s}⎦+2$个不同的增广路径长度，并且相同长度的路径没有公共结点。
　　那么定义以下算法：
　　image
　　最短增广路径是相对于当前匹配集合M而言的，比如M是空集的时候，能找到的最短增广路径长度应该是1。
　　也就是说我们通过最多执行$2⎣ \sqrt{s}⎦+2$次上图步骤1即可找到最大匹配。
　　有了前面匈牙利算法的基础，KM算法重点就是理解如何找到最短增广路径。

模板代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <cmath>
using namespace std;
 
const int MAXN = 3010;
const int MAXM = 3010*3010;
const int INF = 0x3f3f3f3f;
 
struct Edge
{
	int v;
	int next;
}edge[MAXM];
 
struct node
{
	double x, y;
	double v;
}a[MAXN], b[MAXN];
 
int nx, ny;
int cnt;
int t;
int dis;
//first记录Edge链表的头结点，通过Edge.next存储所有u的关系边。
int first[MAXN];
int xlink[MAXN], ylink[MAXN]; 
/*xlink[i]表示左集合顶点所匹配的右集合顶点序号，ylink[i]表示右集合i顶点匹配到的左集合顶点序号。*/
int dx[MAXN], dy[MAXN]; 
/*dx[i]表示左集合i顶点的距离编号，dy[i]表示右集合i顶点的距离编号*/
int vis[MAXN]; //寻找增广路的标记数组 
 
void init()
{
	cnt = 0;
	memset(first, -1, sizeof(first));
	memset(xlink, -1, sizeof(xlink));
	memset(ylink, -1, sizeof(ylink));
}
 
void read_graph(int u, int v)
{
	edge[cnt].v = v;
	edge[cnt].next = first[u], first[u] = cnt++;
}
//找出当前匹配的最短增广路径长度
int bfs()
{
	queue<int> q;
	dis = INF;
	memset(dx, -1, sizeof(dx));
	memset(dy, -1, sizeof(dy));
	for(int i = 0; i < nx; i++)
	{
		if(xlink[i] == -1)
		{
			q.push(i);
			dx[i] = 0;
		}
	}
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		if(dx[u] > dis) break;
		for(int e = first[u]; e != -1; e = edge[e].next)
		{
			int v = edge[e].v;
			if(dy[v] == -1)
			{
				dy[v] = dx[u] + 1;
				if(ylink[v] == -1) dis = dy[v];
				else
				{
					dx[ylink[v]] = dy[v]+1;
					q.push(ylink[v]);
				}
			}
		}
	}
	return dis != INF;
}
//匈牙利算法寻找增广路径，不过要限制增广路径的长度。
int find(int u)
{
	for(int e = first[u]; e != -1; e = edge[e].next)
	{
		int v = edge[e].v;
		if(!vis[v] && dy[v] == dx[u]+1)
		{
			vis[v] = 1;
            //在这里限制路径长度
			if(ylink[v] != -1 && dy[v] == dis) continue;
			if(ylink[v] == -1 || find(ylink[v]))
			{
				xlink[u] = v, ylink[v] = u;
				return 1;
			}
		}
	}
	return 0;
}
 
int Hopcroft-Karp()
{
	int ans = 0;
    //while循环最多执行2s^0.5 + 2次即可找到最大匹配，每次bfs这个过程最复杂的情况就是遍历完所有结点。
	while(bfs())
	{
		memset(vis, 0, sizeof(vis));
        //由于长度相同的增广路径没有公共节点，for循环中find函数最坏情况只是遍历完所有的关系边。
		for(int i = 0; i < nx; i++) if(xlink[i] == -1)
		{
			ans += find(i);
		}
	}
	return ans;
}
 
int main(int argc, const char * argv[]) {
    int u, v, k;  //u和v是临时变量，k表示关系边的数量
    init();
    scanf("%d%d%d", &nx, &ny, &k);
    //录入关系边
    while (k--) {
        scanf("%d%d", &u, &v);
        read_graph(u, v);
    }
    printf("%d\n",Hopcroft-Karp());
    return 0;
}