前言
搜索算法是利用计算机的高性能来有目的地穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。
二分搜索
假如有若干个有序整数,我们需要从这个序列中中查找我们是否有我们想要的数字。
2 3 4 5 6 8 12 20 32 45 65 74 86 95 100
比如我想知道这个序列中有没有25这个数字?正常情况,我们会想到从头到尾或者从尾到头遍历查找。
数据量大的情况下顺序遍历确实太慢了,而且我们已经确定了这个序列的 单调性 的情况下,那么有以下搜索方式:
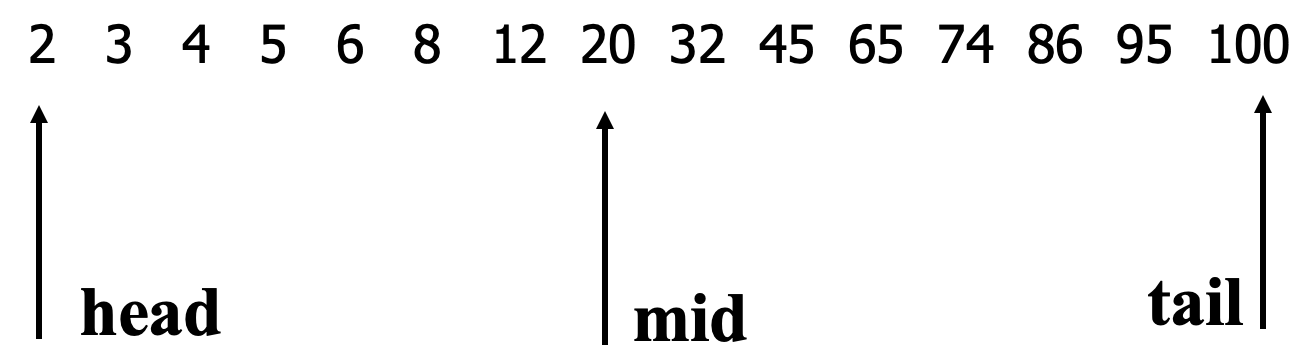
->head和tail表示首尾坐标,如果head > tail 退出循环。
mid = (head + tail) / 2,查看mid坐标对应的元素是否满足条件?
1.如果mid元素满足条件,记录当前mid坐标退出循环。
2.如果mid元素的值大于目标元素,tail = mid,返回步骤->。
3.如果mid元素小于小于目标元素,head = mid,返回步骤->。
三分搜索
如果数据在指定区间内不具备单调性,但是满足 凸性 (先递增后递减或者先递减后递增)。
这种情况我们可以使用三分搜索找到极值(极大或者极小)。
假设要在一个区间内找到极大值,先把整个区间三等分,出现以下情况:
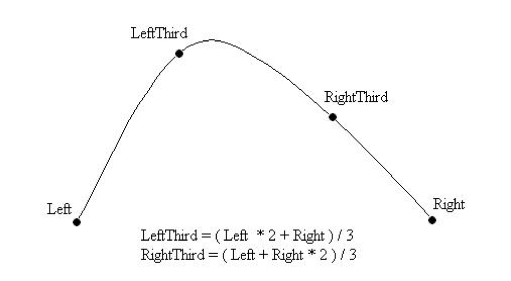

如果是LeftThird的值大于等于RightThird的值,极值在右边两个区间内。Left = LeftThird,继续三分。


如果LeftThird的值小于RightThird的值,极值在左边两个区间内。Right = RightThird,继续三分。
深度优先搜索
基本思想:从初始状态S开始,利用规则生成搜索树下一层任一个结点,检查是否出现目标状态G,若未出现,以此状态利用规则生成再下一层任一个结点,再检查是否为目标节点G,若未出现,继续以上操作过程,一直进行到叶节点(即不能再生成新状态节点),当它仍不是目标状态G时,回溯到上一层结果,取另一可能扩展搜索的分支。生成新状态节点。若仍不是目标状态,就按该分支一直扩展到叶节点,若仍不是目标,采用相同的回溯办法回退到上层节点,扩展可能的分支生成新状态,…,一直进行下去,直到找到目标状态G为止。
算法步骤:
(1)把起始节点S线放到OPEN表中。
(2)如果OPEN是空表,则失败退出,否则继续。
(3)从OPEN表中取最前面的节点node移到CLOSED 表中。
(4)若node节点是叶结点(若没有后继节点),则转向(2)。
(5)扩展node的后继节点,产生全部后继节点,并把他们放在OPEN表的前面。各后继结点指针指向node节点。
(6)若后继节点中某一个是目标节点,则找到一个解,成功退出。否则转向(2)循环。
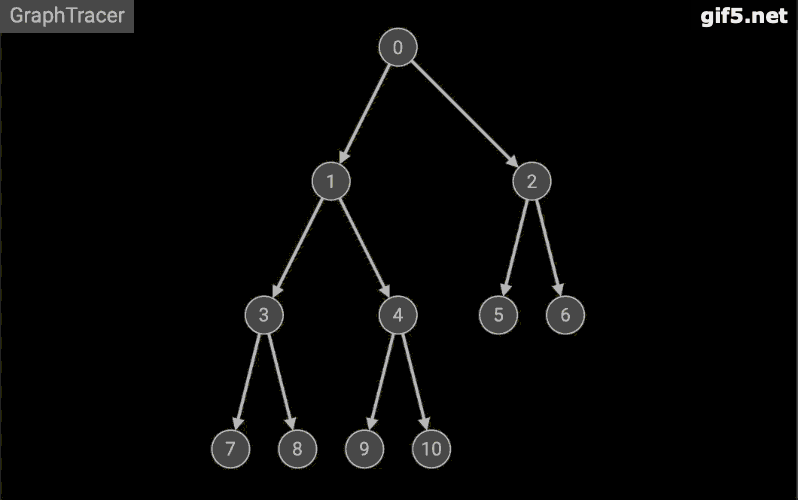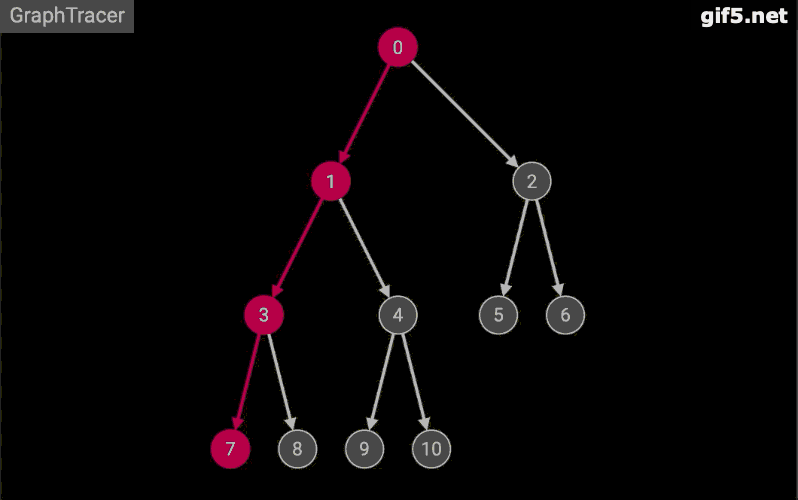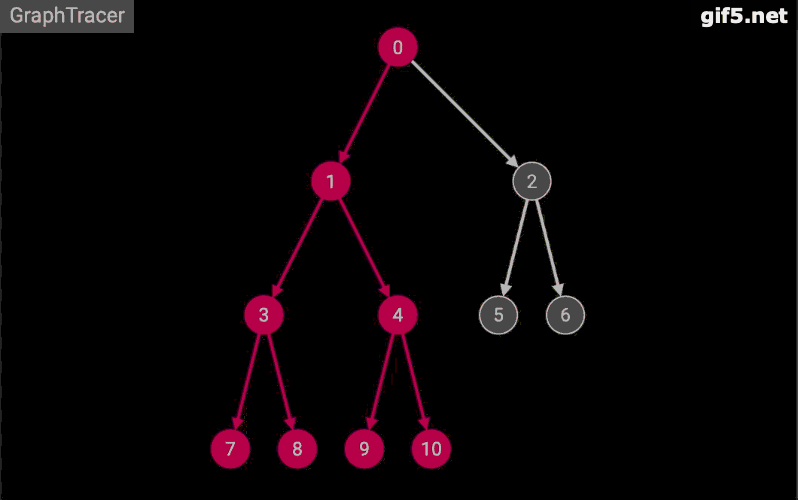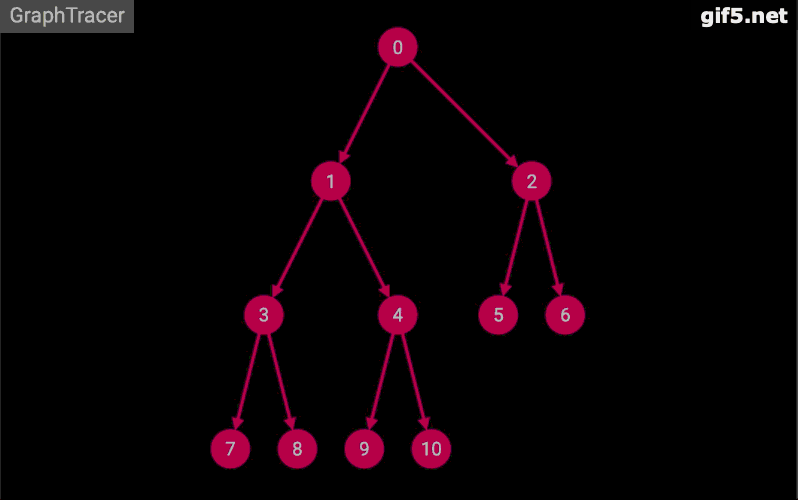
广度优先搜索
基本思想:从初始状态S开始,利用规则,生成所有可能的状态。构成树的下一层节点,检查是否出现目标状态G,若未出现,就对该层所有状态节点,分别顺序利用规则。生成再下一层的所有状态节点,对这一层的所有状态节点检查是否出现G,若未出现,继续按上面思想生成再下一层的所有状态节点,这样一层一层往下展开。直到出现目标状态为止。
算法步骤:
(1)把起始节点S线放到OPEN表中
(2)如果OPEN是空表,则失败退出,否则继续。
(3)在OPEN表中取最前面的节点node移到CLOSED 表中。
(4)扩展node节点。若没有后继(即叶节点),则转向(2)循环。
(5)把node的所有后继节点放在OPEN表的末端。各后继结点指针指向node节点。
(6)若后继节点中某一个是目标节点,则找到一个解,成功退出。否则转向(2)循环。