前言
前段时间我读了Jeff教授算法文章后受益颇多,所以决定根据他的每个知识点做一些学习记录。一来我可以提升自己的翻译能力,再者记录一些重要知识点方便回顾。
知识点
约化
约化是算法设计过程中最通用的方法。将问题X约化成问题Y意味着使用Y的算法作为一个黑盒子或者子程序来写X的算法。最重要的是X算法的正确性并不取决于Y算法是如何运作的。我们唯一能假设的是Y算法可以正确解决问题。在这个黑盒子内部是如何运作的并不是我们所关心的。
当我们在设计算法的时候,我们不需要知道所使用的的子程序是如何实现的,也不需要担心我们的算法又会被当成子程序来解决什么别的问题。这种忽视往往给初学者带来不适感,但这样却又是不可避免且极其有用的。
简化和代理
递归就是一种特别有用的约化,粗略描述如下:
•如果有一个问题实例可以被直接解决,那就直接解决它。
•反之,将它约化成一个或者多个更简单且相同的问题实例。
如果这里的自我引用(上述加粗部分)让你感觉到困惑,你将这些更简单的问题代理给“别人”会来解决,就像你可以假设其他类型的约化一样。现在你仅有的任务就是简化原问题,或者如果不需要进行简化就直接解决它;“别人”将会为你解决这些更简单的子问题,这里正如前文所提到的我们不需要关注子程序内部是如何实现的。富有数学经验的读者或许已经认出这个“别人”有一个更通俗的名称:归纳假设。
递归方法不能是无限循环的,最终这种循环都会导向一个可被解决的基础方案。满足这个条件的通用方法就是约化出一个或者多个范围更小且相同的问题实例。
归并排序
归并排序的大致步骤如下:
1.将输入数组尽量分为大小相等的两个子数组。
2.对每个子数组进行归并排序。
3.将两个有序的子数组合并为一个。
下图是归并排序的伪代码:
正确性
为了证明这个算法是正确的,我们需要使用两次归纳法,先证明Merge这个子程序,再证明Mergesort算法。
引理1.1. 假设输入的子数组都是排好序的,Merge操作正确地合并子数组A[1..m]和A[m+1..n]。
证明: 设A[1..n]为任意数组,m是任意整数,并且A[1..m]和A[m+1..n]都是有序的。我们可以证明对于所有的k∈[0..n],主循环中最后的n-k-1次迭代正确地将A[i..m]和A[j..n]合并到了B[k..n],这个证明是基于对n-k+1个剩余合并元素的归纳。
如果k>n,这个算法已经成功合并这两个数组了。反之,在主循环中第k次迭代我们需要考虑四种情况。
•如果j>n,子数组A[j..n]中的元素遍历完了,那么当前最小的元素就是A[i]。
•如果i>n,子数组A[i..m]中的元素遍历完了,那么当前最小的元素就是A[j]。
•否则如果A[i]<A[j],那么当前最小的元素就是A[i]。
•否则我们将得到当前最小的元素是A[j]。
在所有的情况中,B[k]都正确分配到了A[i..m]和A[j..n]的最小元素。在A[i]赋值到B[k]的两种情况中,通过归纳假设可以知道剩下的n-k次迭代可以正确的将A[i+1..m]和A[j..n]中元素正确地合并到B[k+1..n]中。同样,其他两种情况也是这样的。
定理1.2. MergeSort正确地对数组A[1..n]进行了排序。
证明: 这里通过对n归纳假设来证明。如果n<=1,这个算法不需要做任何操作。不然,通过归纳假设可以知道在子数组A[1..m]和A[m+1..n]成功合并到一个有序数组后(由引理1.1可知),我们的算法就可正确的对两个子数组进行排序。
分析
由于MergeSort是递归的,它的运行时可以表示为一个递推式。Merge操作耗费的时间为O(n),因为它的循环操作都是常量级别的。我们立马可以得出MergeSort的递推式如下:
就像大多数分而治之的递推式一样,我们可以放心的去掉取整符号(领域变换,下面的小节会讲到),从而得到一个更加简单的递推式$ T(n)=2T(n/2)+O(n)$。通过递归树方法的一种情况(后面小节的内容)可以立马得到闭型表达式$ T(n)=O(n logn)$。即使你现在还不了解递归树,也可以通过归纳假设来验证这个表达式。
快速排序
快速排序的大致步骤如下:
1.从数组中选择一个游标元素。
2.将数组分为三个子数组,包括三种情况小于、等于、大于游标元素。
3.递归地对第一和第三个子数组快速排序。
下图是快速排序的伪代码: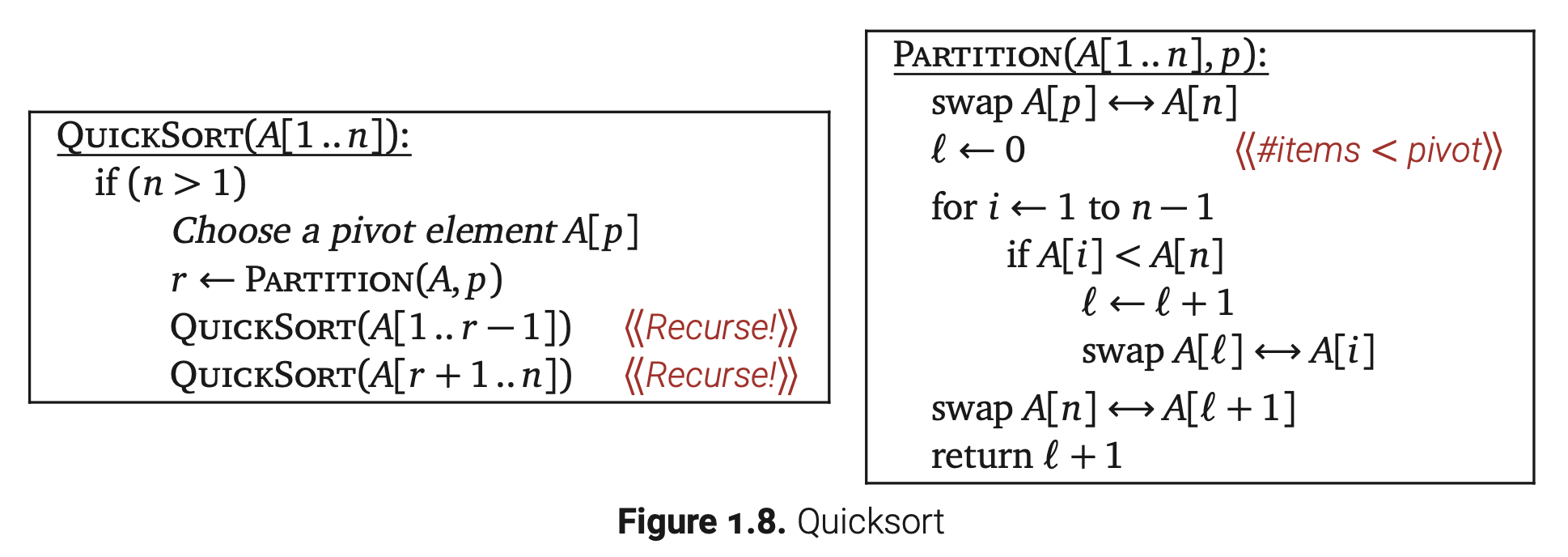
正确性
验证过程和归并排序类似,也是通过两次归纳法证明。先证明Partition方法正确地将数组划分,再证明Partition方法正确的情况下,QuickSort的排序也是正确的。
分析
分析过程也和归并排序差不多,Partition的运行时间为O(n),我们可以得到一个关于r(游标元素在数组中的排位)的递推式
如果我们每次都能将游标元素定位在中间,均分出两个子数组,递推式就变成
这样它的效率就和归并排序一样了。
实际上,r的取值在1到n之间,那么有
极端情况下,两个子问题完全不平衡—甚至r=1或者r=n—那么递推式就变成$T(n)\leq T(n-1)+O(n)$。结果就变成了$T(n)=O(n^2)$。
直觉告诉我们r大概率是在n/10和9n/10之间的,那么平均的运行时间应该是$O(n log n)$。
模式
通过前面的例子,我们为分治方法设立三个步骤:
1.分解:将原问题分解成为几个独立的子问题。
2.代理:通过归纳假设来解决每个子问题。
3.联合:将每个子问题的方案结合来解决原问题。
如果子问题的运行时在常量级别内,那就直接暴力解决。
验证一个分治方法是否正确通常会使用归纳法,至于如何分析运行时就需要用到递归树了。
递归树
递归树是一种用来解决分支问题的工具,具有简单、普遍、形象等特点。它的每个节点对应着一个递归子问题。节点的值就表示对应的子问题所花费的时间,不包括递归调用。这样所有节点的值加起来就是整个算法的运行时。
为了让这个概念变得具体,你可以想象一个还未计算递归的分治算法耗费时间为$O(f(n))$,接下来他做了r次递归调用,每一次的范围是n/c。如果忽略常数因子(隐藏$O()$这个记号),那么这个算法的运行时可以表示为如下的递推式:
递归树的根节点代表$T(n)$,它的节点值为$f(n)$,还带有r个子节点,这些子节点可以看做新的递归树的根节点$T(n/c)$。递归树是一棵r叉树,高度为d的节点的值为$f(n/c^d)$。递归树画出来是下面这样的: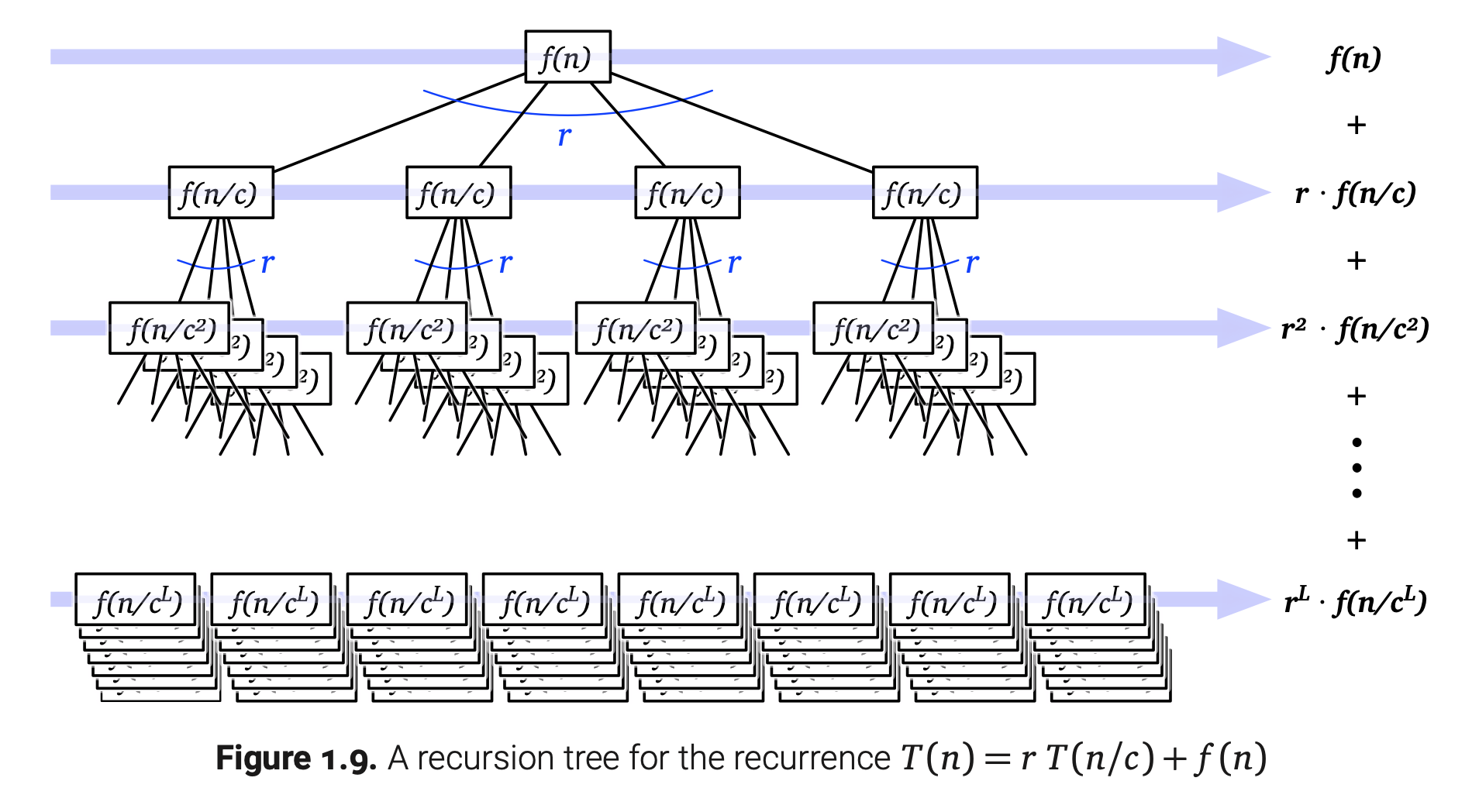
递归树的节点对应着递推式展开过程中的项。因为我们只需要找一个渐进的边界(递归的结束条件),假设对于所有的$n\leq n_0$有$T(n)=1$,那么$n_0$可以是任何一个正数常量。通常来说,我们会选择最适合分析的$n_0$。对于这个例子,$n_0=1$是最合适的。
现在$T(n)$就等于递归树所有子节点值相加之和。如果分层来看,对于每个正数i,第i层有$r^i$个节点,么个节点的值为$f(n/c^i)$。那么,
L是树的高度。由我们递归的结束条件$n_0=1$,可以退出$L=log_cn$,因为$n/c^L=n_0=1$。接下来便可得知叶节点的数量$r^L=r^{log_cn}=n^{log_cr}$。那么最后一层的和就是$n^{log_cr}·f(1)=O(n^{log_cr})$,因为$f(1)=O(1)$。
这里我通过逐层评估通项会发现有三种情况:
•递减:如果逐层比较通项出现指数级衰减(r < c)—每个通项是常数因子且比前一项小—那么$T(n)=O(f(n))$。在这种情况,根节点的值在求和结果中占主导地位。
•相等:如果每个通项都相等(r = c),我们马上可以得出$T(n)=O(f(n)·L)$。(常数c就消失在$O()$记号中了)
•递增:如果逐层比较通项出现指数级增长(r > c)—每个通项是常数因子且比前一项大—那么$T(n)=O(n^{log_cr})$。在这种情况,叶节点层的值在求和结果中占主导地位。
在第一和第三种情况下,只有几何级数最大的通项起到了作用;所有别的通项都被$O(·)$隐藏掉了。在递减的情况下,我们不需要计算L;如果递归树是无穷的,渐进的上界依然有效。
递归树技术也可以用在范围不同的循环子问题算法中。比如,快速排序的游标总是落有序数组的三分之一处,那么最坏运行时将会满足递推式
这个递推式也许看起来可怕,但实际上还是很平常的。如果我们画几层递归树来看,就会很快发现每一层的节点值之和不超过n — 越深的层将会失去一些节点 — 这棵树的高度为$log_{3/2} n=O(log n)$。那么马上可以得出$T(n)=O(n log n)$。(如果只算节点完整的层数应该是$log_3 n=Ω(log n)$,但是在这种保守分析只能增大一个常数因子,对于我们来说一点都不重要。)事实上递归树是否平衡对我们的分析并没有实际影响。
作为一个比较特殊的例子,快速排序最坏的递推式$T(n)=T(n-1)+T(1)+O(n)$给了我们一颗完全不平衡的递归树,所有非叶节点的子节点中有一个是叶节点,它逐层的和并不在我们前面提到的三种情况中,但是我们还是可以得出答案$T(n)=O(n^2)$,通过观察发现每层的值最大是n且最多只有n层。(我们再次发现保守分析并不重要,因为有n/2层的值是不低于n/2的)
忽略向上和向下取整
细心的读者也许会反对我们的分析掩盖了一个重要的细节。归并排序的运行时并没有严格遵守递推式$T(n)=2T(n/2)+O(n)$;毕竟输入大小n可能是一个奇数,那么一个非整数大小的数组排序有什么意义呢?完整的归并排序递推式是比较难以处理的:
当然,我们可以通过归纳法来验证$T(n)=O(n log n)$,但是这将通过非常可怕的必要计算。幸运的是有一个简单的技术可以从地推始终移除向上和向下取整,它叫做领域变换。
•首先,因为我们是要得到一个上界,可以安全的高估T(n),只要假装两个子问题的大小是相等的,然后再消除向上取整:
•其次,我们定义一个新的函数$S(n)=T(n+α)$,利用常数α让S(n)满足一个简单的递推式$S(n)\leq 2S(n/2)+O(n)$。为了找到一个合适的α,我们从已经给出的T递推式得到S递推式:
令α=2将递推式简化成$S(n)\leq 2S(n/2)+n+2$,这正是我们想要的。
•最后,由这个递推式可以得出$S(n)=O(n log n)$,因此
领域变化可以用来为任何分治递推式移除取整和低位项。但是我们不再需要如此麻烦地验证这些细节问题了!从现在起,遇到分治递推式就可以直接忽略掉取整和低位项了。
线性时间内查找
快速查找
快速查找使用快速排序中的Partition方法,伪代码如下:
快速查找的最坏运行时和快速排序很相似。
用l表示递推子问题的范围大小,我们可以将此递推式简化如下:
如果游标元素总是数组总的最大或者最小元素,那么这个递推式就能简化为$T(n)=T(n-1)+O(n)$,他表示$T(n)=O(n^2)$。
好游标
如果我们可以选择一个好游标,就可以避免上面二次项式的情况,这表示$l\leq αn$,常数α<1。那么递推式进一步简化为
这个递推式发展成了逐层几何级数衰减,这就表示递归树根节点的值主导结果,那么$T(n)=O(n)$。
换句话说,如果我们能在线性时间内找到靠近中间的元素,也就能在线性时间内准确找到中间元素。假设我们数组分为每五个元素一块,蛮力求解每个块的中间元素,将他们收集在数组$M[1..\lceil n/5\rceil]$,然后从M中找一个中间元素。最后我们将这个块的中间元素作为快速查找的游标。伪代码如下:

MomSelect使用递归有两个目的;一个是选择游标元素,另一个是目标元素在游标元素的哪一端。
分析
但是为什么这么做比较快呢?首先可以想到的是中间的中间元素Mom是一个好游标。Mom比M数组中一半($\lfloor \lceil n/5\rceil /2 \rfloor ≈ n/10$)的元素大,每一个块的中间元素又比块中的另外两个元素大。那么Mom至少比整个数组中3n/10的元素大;同样地,Mom也至少比整个数组中3n/10的元素小。最坏情况下,第二次递归的范围是7n/10。接下来写出递推式
如果我们画出递归树,我们观察到每层递归树的计算范围是前一次范围的9/10。这说明每层节点和呈现指数级衰减,那么$T(n)=O(n)$。
理性核实
可能大家都想知道为什么分块大小是5?答案是5是构成指数级衰减递归树的最小奇数。如果我们的分块大小是3,那么运行时递推式就是
这个式子在前文中已经见过了,分块大小为3并不能在线性时间内查找到元素。
通过严格分析我们会发现$O()$记号隐藏的常数相当大,如果我们只记录比较运算。从五个元素中找出中间元素,最多需要6次比较,所以我们需要经过6n/5次比较才能启动递归子问题。Partition操作需要n-1次比较,但是我们已经知道了3n/5的元素或大或小与游标元素,那么Partition实际上只需要2n/5次比较。这样,一个更详细的最坏比较递推式就是
通过递归树方法得出上界
实际上,这个MomSelect并非真的就是最坏情况分析预测的这么慢,毕竟不可能每次递归都选到最坏的游标。
结语
最近在看罗素的《哲学问题》,有条评论说“科学研究有两大利器,归纳和演绎”。读完Jeff教授的文章我对此也深感认同,因为原文多处理论都是通过归纳假设来证明的,而且后面有留有一半的篇幅是练习题留给读者思考(多数需要证明题目以便解答后续的问题)。
原文链接
http://jeffe.cs.illinois.edu/teaching/algorithms/book/01-recursion.pdf