前言
根据以前的ppt和笔记资料,我应该是学过prim和kruskal算法的。但是现在我已经忘完了,一点印象都没有了。唉!再看一遍。
知识点
假设已知一个无向连通加权图。这个图G=(V,E)有一个函数$w:E→R$,w(e)表示每个边有一个实际的权值,可能是正的、负的或者是0。这一章会介绍几个算法来寻找G的最小生成树,生成树T的最小化函数如下:
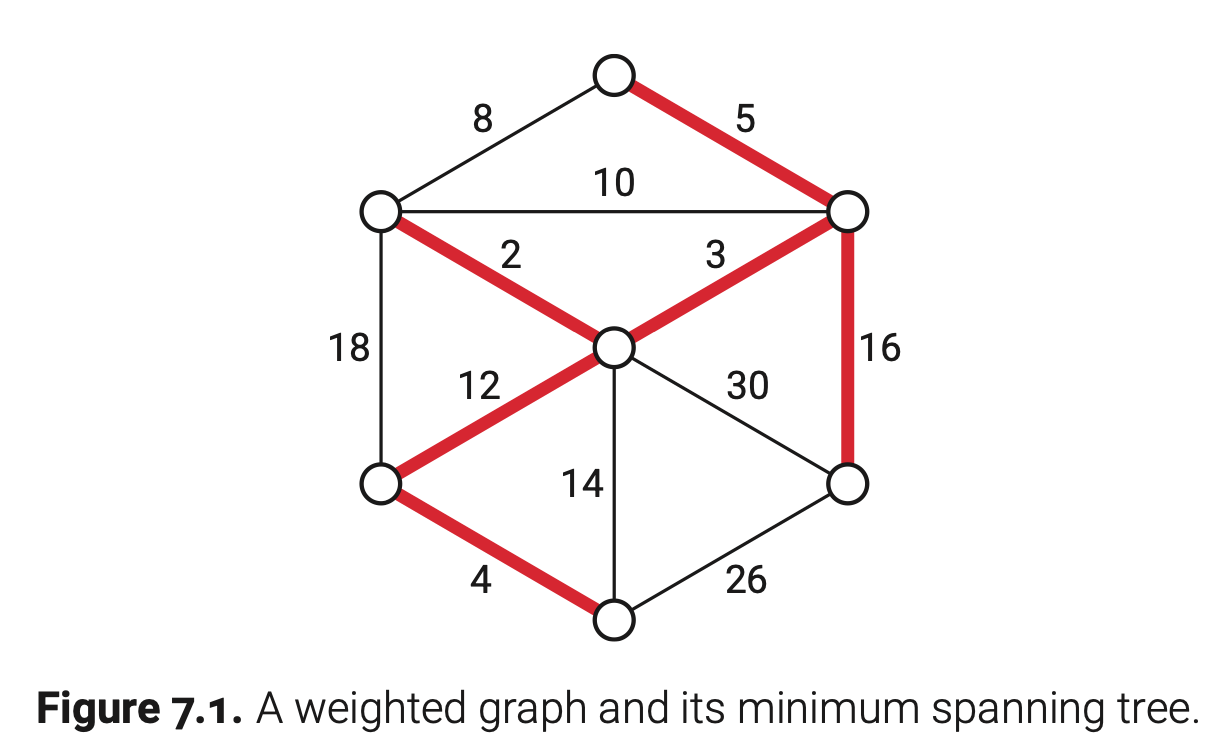
不同的边权值
这个问题中有个需要注意的点是,加权图可以有多个具有相同最小权值的生成树;特别是,如果G中每条边的权值都是1,那么每个G的生成树都是一个最小生成树,权值是V-1.这种不明确使我们开发算法变得复杂;如果我们可以假设最小生成树是唯一的,那么问题就会相对简单些。幸运的是,正好有一个方案保证了我们所需的唯一性。
引理7.1. 如果图G中所有边的权值都是不同的,那么G有一棵唯一的最小生成树。
证明: 假设G是任意一个有两棵最小生成树T和T’的连通图;我们需要证明G中有一些边具有相同的权值。这个证明是基于贪心交换论证的。
每个我们的生成树都必须包含一条其他生成树缺少的边。让e表示T\T’(T包含,T’缺少)中的一条权值最小的边,用e’表示T’ \T中的一条权值最小的边。为了不失普遍性,假设$w(e)≤w(e’)$。
子图$T’∪\{e\}$包含了一个环路C,正好经过边e。用e’’表示这个环路中任意一条不在T中的边。因为T是一棵树,至少有一条这样的边存在。(我们可能得到e’=e’’,也可能不会)因为e∈T,我们知道$e’’≠e$并且因此e’’∈T’ \T。接着就有了$w(e’’)\geq w(e’)\geq w(e)$。
现在考虑生成树$T’’=T’+e-e’’$。(这棵新的树T’’可能和T相同)我们立刻得到$w(T’’)=w(T’)+w(e)-w(e’’)\leq W(T’)$。但是T’是一棵最小生成树,我们必须有$w(T’’)=w(T’)$;换句话说,T’’也是一棵最小生成树。我们得出结论:w(e)=w(e’’),这个结果完成了我们的证明。
如果我们已经有一个用在不同的边权值的算法,那也可以把它用在有相同权值边的图中,只要我们有统一的方法来打破平衡。下面就由一个算法可以取代简单的权值比较。ShortEdge使用四个整数i、j、k、l作为输入,代表着四个不同的顶点,并且它可以决定两条边(i,j)和(k,l)中那一条具有“最小”权值。(因为输入图是无向的,所以(i,j)和(j,i)表示同一条边)
根据引理7.1和这个打破平衡的规则,我们将会安全的假设剩下章节中的边权值总是不同的,因此最小生成树总是唯一的。特别是,我们可以没有疑虑地自由讨论特指的最小生成树。
唯一的最小生成树算法
有很多算法可以计算最小生成树,但是它们几乎都是采用了下面这个通用策略。这个情况和图的遍历很相似,几个不同算法的变化部分都是通用图遍历算法的任意优先搜索。
这个通用的最小生成树算法维护了一个输入图G的无环子图F,我们将之称为中间生成森林。在整个过程中,F满足一个不变性:F是G的最小生成树的一个子图。
最初F是一棵V个单节点树组成。这个通用算法通过添加它们之间确定的边来连接F中的树。当这个算法停止时,F中只有一棵生成树;我们的不变性告诉我们这一定是G的最小生成树。显然,我们需要很小心地确定哪条边可以用来演变森林,因为并不是所有的边都在最小生成树中。
在这个演变过程中的任意阶段,中间生成森林F会从剩余图中引入两种类型的边。
•无用边:一条边不在F中,但是它的两个端点都在F的同一分量中。
•安全边:一条边是当前权重最小的,并且它在同一分量中只有一个端点。
同一条边可能对与两个不同分来来说都是安全的,一些G\F中的边既不是安全也不是无用的;我们称之为未决定的。
所有最小生成树的算法都是基于这两个简单的观察。第一个观察是RobertPrim在1957年证明的(尽管几个早期的算法已经有所暗示),第二个是直接得到的。
引理7.2(Prim). G的最小生成树包含了每一条安全边。
证明:实际上我们可以证明一个更有力的命题:对于任意G的顶点子集S,G的最小生成树包含了一条最小权值边,它恰好有一个端点在S中。就像前面的引理一样,我们使用贪心交换论证来证明这个命题。
假设S是任意一个G的顶点子集,用e表示恰好有一个端点在S中并且权重最小的边。(前面提到过所有边得权值不同,所以e是唯一的)用T表示一棵任意不包含e的生成树;我们需要证明T不是G的最小生成树。
因为T是连通的,它包含了一条从e的一个端点到另一个端点的路径。因为这个路径是从S中的一个顶点到另一个不在S中的顶点,那么它一定包含了至少一条恰好有一个端点在S中的边;用e’表示这条边。因为T是无环的,从T中移除e’会得到一个包含两个分量的生成森林,每个分量都包含了e的一个端点。这样,将边e添加到这个森林中得到一棵新的生成树$T’=T-e’+e$。根据e的定义可知$w(e’)>w(e)$,这就表示T’的权值小于T。这样,T就不是G的最小生成树,如此就完成了证明。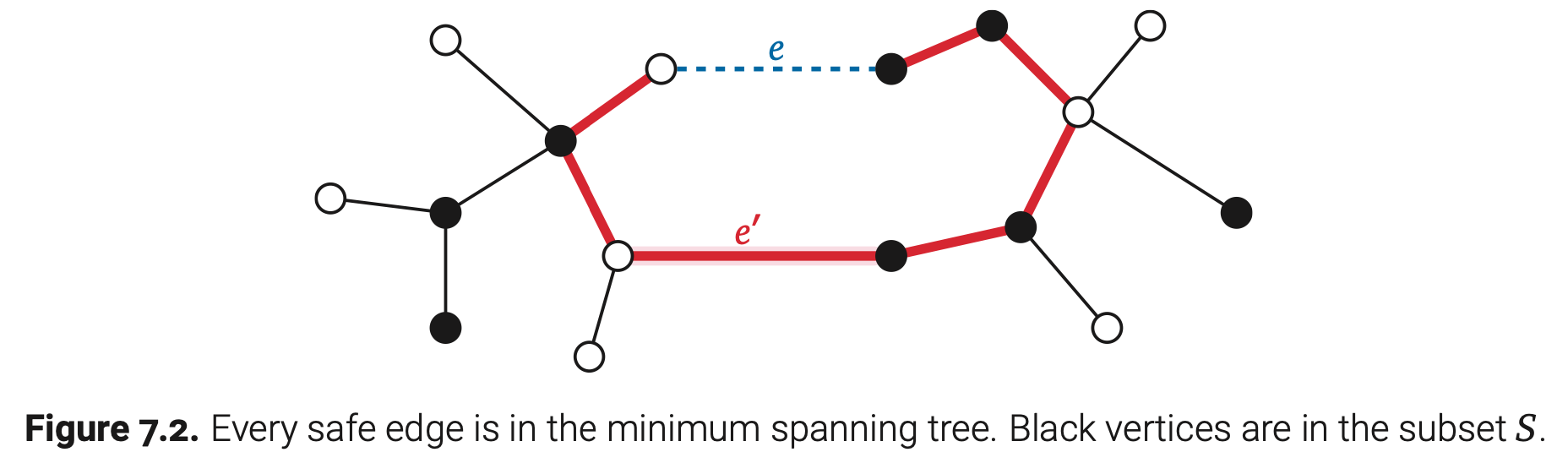
引理7.3. 最小生成树不包含无用边。
证明:在F中增加一条无用边会产生一条环路。
我们的通用最小生成树算法重复地加入安全边来演变森林F。如果F还没有连通,那至少会存在一条安全边,因为输入图G是连通的。这样,在每次迭代中不管我们加入的是哪一条安全边,我们的通用算法最终都会使F连通。根据归纳法,引理7.2表明最终得到的树实际上就是一棵最小生成树。无论何时我们在F中加入一条新边,一些未决定的边就会变成安全边,另一些未决定边会变成无用边。(只要一条边变成无用的,那么他的状态就不会改变了)为了完全指定一个详细的算法,我们必须决定在每次迭代中哪一条安全边被加入,怎么找到这些边。
Boruvka算法
在1926年最古老且简单的最小生成树算法被捷克数学家Otakar Boruvka所发现,也就是大约在Jindrich Saxel问了他如何用最少的电线构造一个连通一些城市的电路网络之后的一年。后来又陆续被一些其他人发现,这里就不详细介绍了。Boruvka算法可以被总结为一条:添加所有的安全边和递归。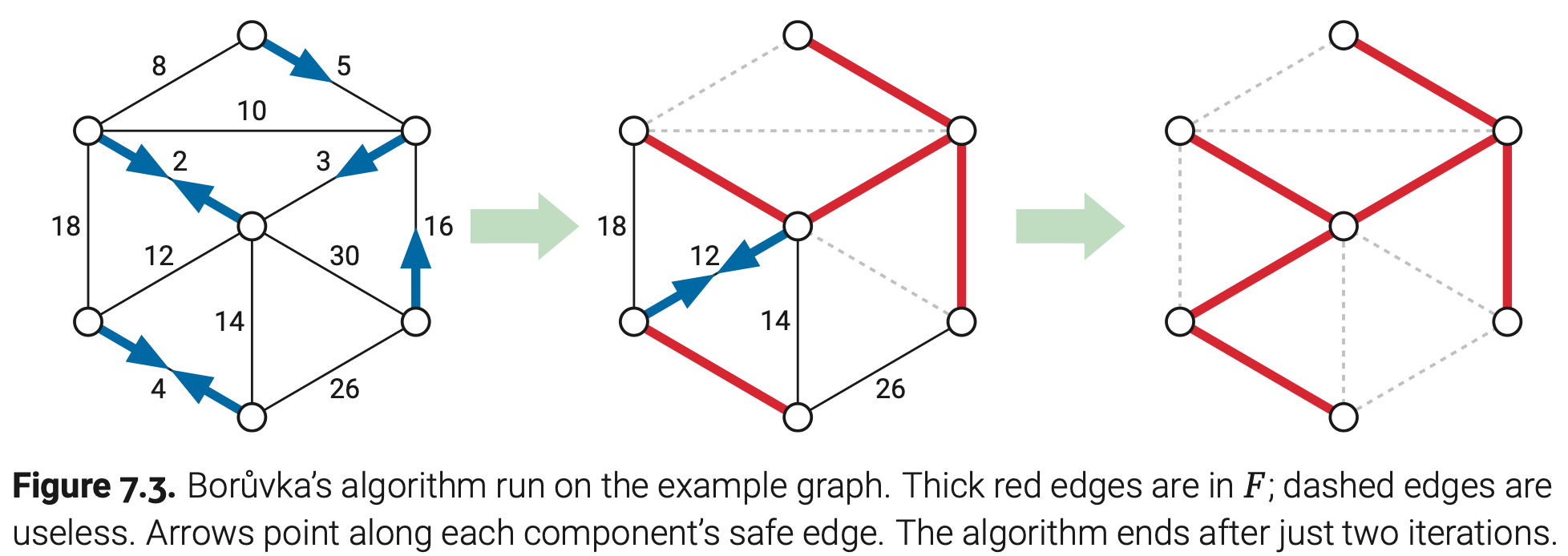
接着多讲一些Boruvka算法的细节。这个算法调用了第五章CountAndLabel算法来计算F的分量个数,每个顶点有一个整数标记comp(v)表示它所在的分量。
现在只剩下如何鉴定和加入安全边到F中,假设F有不止一个分量,不然我们就已经结束了。通过暴力检测G中的每条边,接下来的子程序计算了一个安全边的数组safe[1..V],safe[i]有一个端点在F的第i个分量的最小权重边。另外,我们将边uv的权重与safe[comp(u)]和safe[comp(v)]比较,如果有必要就更新数组。只要我们鉴定完了所有的安全边,我们就把每个safe[i]的边加入F。
每次调用CountAndLabel的执行时间为O(V),因为F最多有V-1条边。AddAllSafeEdges运行时间为O(V+E),因为我们花在G中的顶点和边以及F中分量上的时间都是常数级的。因为输入图是连通的,我们有V≤E+1。这表明每次Boruvka方法的每次while循环迭代耗时为O(E)。
在最坏的情况下(恰好出现两两分量成对合并),每次迭代至少可以将F的分量数减少一半(递减因子为2)。因为F一开始有V个分量,while循环最多执行O(log V)。我们得出结论Boruvka算法的最终运行时为O(E log V)。
这就是你想要的最小生成树(MST)算法
尽管它的起源比较模糊,早期的西方算法研究者都知道Boruvka算法,但是都误以为它塔复杂了。结果,即使它朴素高效,大多数算法和数据结构书籍甚至都没有提到过Boruvka算法。这种缺失是一个严重的错误;Boruvka算法具有一些其他经典MST算法不具备的优点。
• Boruvka算法通常会快于它的最坏运行时O(E log V)。但次迭代中F的分量的递减因子远远大于2,所以迭代次数小于最坏情况$\lceil log_2V \rceil$。
• Boruvka算法允许并行;在每次迭代中,每个F的分量都是在独立的线程中处理。这种隐式的并行在多核或者分布式系统运行更快。相比之下,其他两种经典的MST算法本质上都是串行的。
• 一些新一代的MST算法在最坏情况下都比这里描述的经典算法快。所有这些更快的算法都是出自于Boruvka算法。
总之,如果你需要实现一个最小生成树算法,那就使用Boruvka。否则如果你想快速证明一些最小生成树相关的东西,那你确实需要知道接下来的两个算法。
Jarnik(Prim)算法
接下来这个古老的最小生成树算法是在1929年捷克数学家Vojteck Jarnik写信给Boruvka发表的。接下来又是一堆人陆续独立发现这个算法,其中一位就是Prim,还有Kruskal和Dijkstra。
在Jarnik算法中,中间森林F只包含了一个不平凡的分量T;所有其他分量都是独立的点。起初,T是图中的任意一个顶点。算法重复以下步骤知道T扩展到整个图:重复添加T的安全边到T中。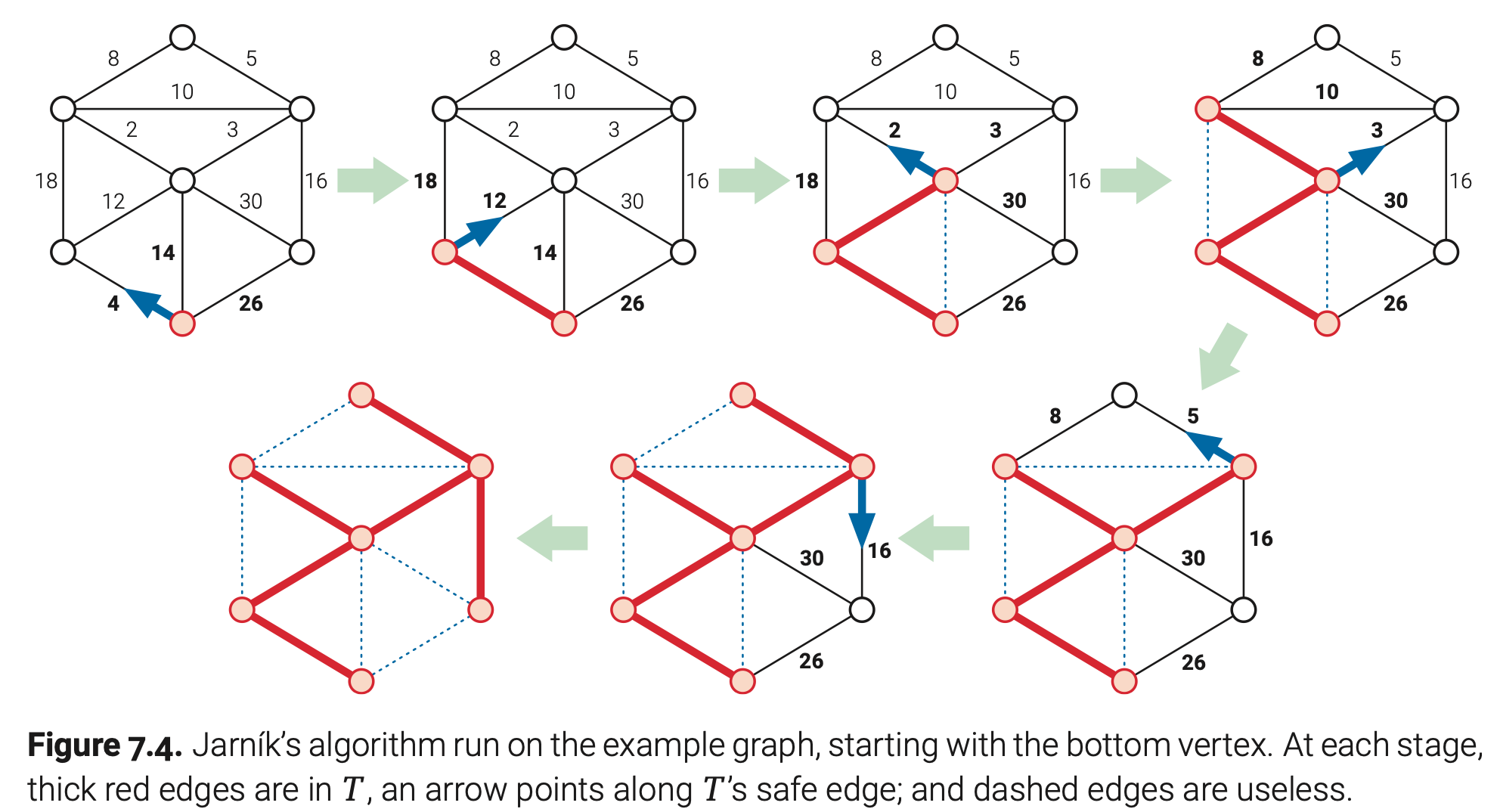
为了实现Jarnik算法,我们T的邻接边都加入到优先队列中。当我们从优先队列中取出最小权值边时,我们首先检查它的两个端点是否在T中。如果不是,我们将这条边加入T并且将新的邻接边加入优先队列。换句话说,Jarnik算法就是第五章末提到的最佳优先搜索的变体!如果我们用标准二进制堆来实现所依赖的优先队列,Jarnik算法的运行时为O(E log E)=O(E log V)。
改进Jarnik算法
我们可以使用一个更复杂的优先队列数据结构斐波那契堆来改进算法,他在1984年被Michael Fredman和Robert Tarjan首次提出。和二进制堆一样,斐波那契堆支持标准优先队列操作Insert、ExtractMin、DecreaseKey。然而不像标准二进制堆,对每个操作的耗时都是O(log n),斐波那契堆支持Insert和DecreaseKey的均摊耗时为常数级,ExtractMin的均摊耗时任然是O(log n)。
为了使用这个更快的数据结构,我们将G的顶点而不是边加入优先队列,顶点v的优先级可能是是它与树T之间的最小权重边,也可能是∞(没有边)。我们可以在算法开始时将所有顶点加入优先队列;然后我们再加入一条新边到T时,我们需要去更新下相邻顶点的优先级。
为了让这段叙述更简单,我们将算法分为两部分。JarnikInit初始化了优先队列;JarnikLoop是主要算法。输入包括了图的顶点和边以及一个起点s。对于每个顶点v,我们需要维护它的优先级priority(v)和最小权重边edge(v),w(edge(v))=priority(v)。
操作Insert和ExtractMin会被调用O(V)次,除了s以外的每个顶点一次,然后DecreaseKey会被调用O(E)次,每条边最多两次。这样,如果我们使用斐波那契堆,这个改进算法的运行时为O(E+V log V),它确实比Boruvka算法快了除非E=O(V)。
然而实际上,这个改进几乎不会比单纯使用二进制堆块,除非输入图非常大且稠密。这个斐波那契堆算法相当复杂,而且运行时间和运行空间中隐藏的常量非常大—也不是无法容忍的,但确实远远超出了二进制堆操作的运行时O(log n)中的常量1。
Kruskal算法
最后一个MST算法是Joseph Kruskal在1956年首次发表的,在这片文章中还有他二次独立发现的Jarnik算法。Kruskal是受到了Boruvka张贴在普林斯顿数学系的一篇机翻原稿的激励。Kruskal发现Boruvka算法中有一些不必要的步骤。同样的算法在1957年被Harry Loberman和Arnold Weinberger再次发现,但不知道何故避免了用他们的名字命名。
和我们早期的最小生成树算法一样,Kruskal算法也有一条令人难忘的描述:通过权重从小到大的顺序遍历边;如果一条边是安全的,就把它加入F。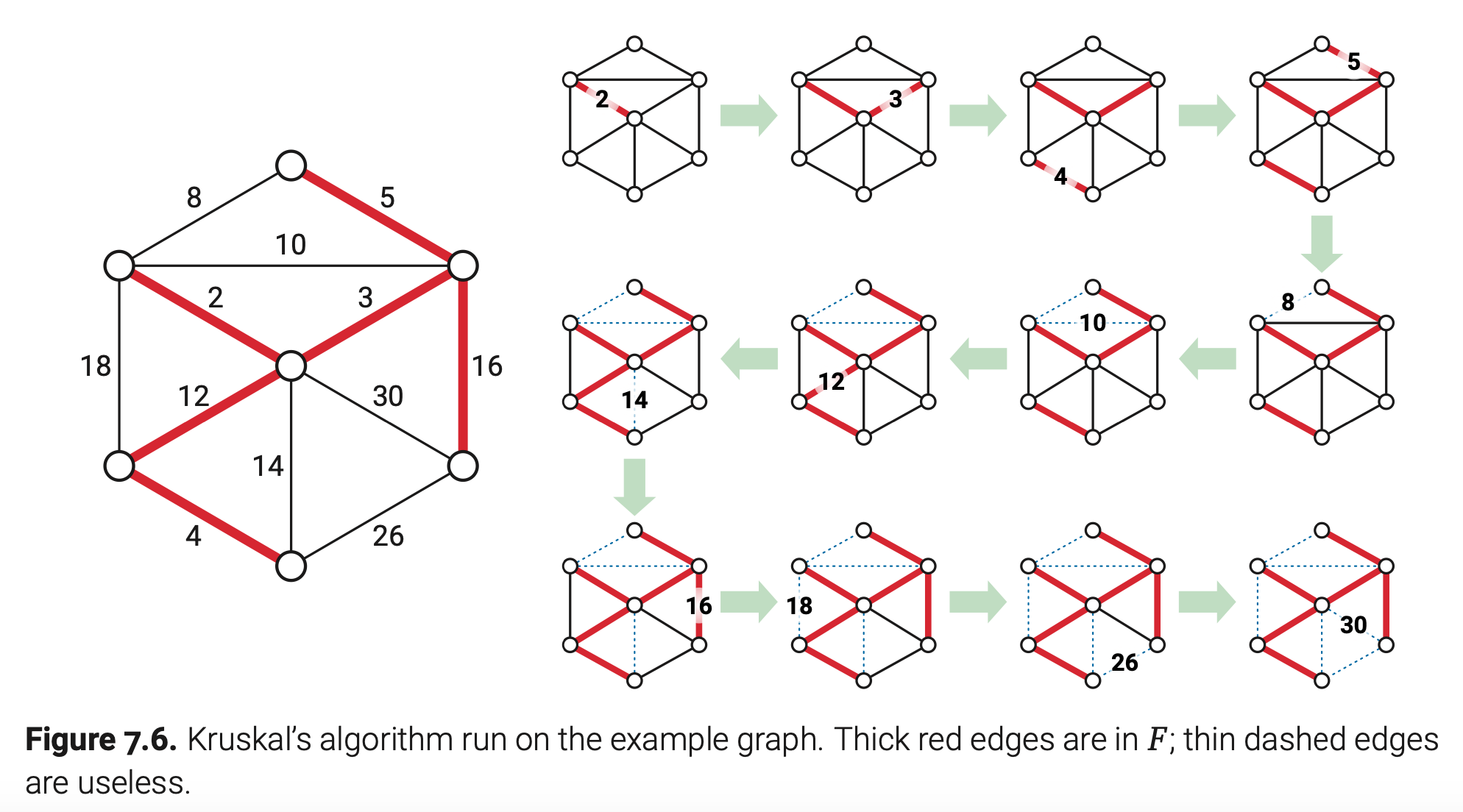
最简单的按边权重从小到大的顺序遍历的方法就是在O(E log E)时间内按边权重排序,然后对这个边的排序列表用一个简单的for循环。很快我们就会看到,这种初步的排序控制了算法的运行时间。因为我们检测边的顺序是按权值从小到大,任意我们检测的边是安全的当且仅当它的端点在F中的不同分量重。假设我们遇到了一条将分量A和B连接起来边e,但它不是安全的。那么一定存在一条更小的边e’,恰好有一个端点在A中。但这是不可能的,因为每个之前检测的边现在两个端点都在F的同一分量中。
就像Boruvka算法一样,每个F的顶点都需要知道它在F的哪个分量中。然而也不同于Boruvka算法,我们不需要在每次添加边后从头计算所有的分量标记。相反,当两个分量被一条边相连时,较小的分量会继承较大分量的标签;就是说,我们遍历较小的分量。对于较小分量中的每个顶点这个遍历需要O(1)时间。每次一个顶点的分量标签改变,F中包含这个顶点的分量会至少增大一倍(递增因子大于2);这样,每个顶点的分量标签最多改变O(log V)次。这表明更新顶点标签的总耗时只有O(V log V)。
一般来说,Kruskal算法将G中的顶点维护在一些分开的不相交子集中(在我们这里,就是F的分量),使用一个数据结构支持一下操作:
• MakeSet(v)—创建一个只包含顶点v的集合。
• Find(v)—返回一个包含v的集合的唯一标记。
• Union(u,v)—将u和v所在的集合合并。
下面就是使用这些操作来完整描述的Kruskal算法:
在初始化排序后,这个算法恰好执行了V次MakeSet操作(每个顶点一次),2E次Find操作(每条边两次),V-1次Union操作(每条最小生成树的边一次)。我们刚才描述的不相交子集数据结构对于MakeSet和Find操作的耗时为O(1),对于Union的均摊耗时为O(log V)。使用这个实现,花在维护集合划分上的总耗时为O(E+V log V)。
但是回想一下仅排序的耗时都已经是O(E log E)=O(E log V)了。因为这个比维护集合划分耗时更大,总的来说我们Kruskal算法的耗时是O(E log V),和Boruvka算法一样,和使用普通堆的Jarnik算法也一样。
结语
这篇好短啊!一天多就搞完了。除了Boruvka算法第一次见,其他两个经典算法我都是学过的。只不过以前是看着模板代码来死记,现在是通过引理推导来理解。而且这些算法的发现者,好多我都有所耳闻。
原文链接
http://jeffe.cs.illinois.edu/teaching/algorithms/book/07-mst.pdf