Jeff Erickson 《Algorithms》08 -- 最短路径

前言

　　我认识它，它不认识我。我笔记里面有Floyd、Dijkstra、BellmanFord和SPFA四个算法，且每个算法下都有思路分析，然而我还是想不起来当初是怎么理解的了。这样看来，我都不知道脑袋里有多少类似的“空中楼阁”。

知识点

假设给我们一个有向加权图G=(V,E,w)和两个顶点，我们想找到从源点s到目标点t的最短路径。也就是，我们想找到从s到t的有向路径P的最小化函数：

$w(P):=\sum\limits_{u\rightarrow v\in P}w(u\rightarrow v)$

比如，现实生活中我们想从一个城市到另一个城市，那么图中的顶点就是城市，边就是道路，权重就是行驶时间，同一条路可能因为方向不同而行驶时间不同。

最短路径树

几乎每个已知的计算一个点到另一个的最短路径算法都是在解决单源最短路径（SSSP）问题：找到从源点s到每个其他顶点的最短路径。这个问题通常是通过找到以s为根的最短路径树来解决，这棵树包含了所有要求的最短路径。
　　不难发现如果每个点的最短路径是唯一的，那么它们就会形成一棵树，因为任意最短路径的子路径本身就是一条最短路径。如果到达某个顶点有多条最短路径，那么我们总是可以选出一条后组合其他路径形成一棵树。如果存在最短路径从s到达两个顶点，先分叉，后合并，在分叉，我们可以不改变长度地修改其中一条，这样两条路径只会分叉一次。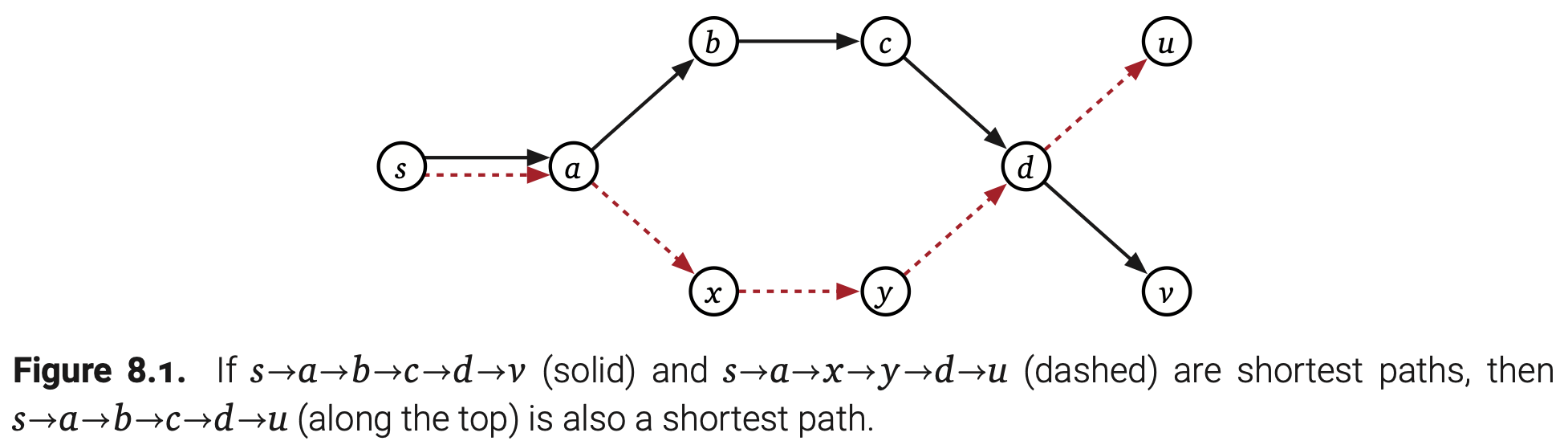

　　尽管最小生成树和最短路径树都是最佳生成树，但它们却不是一个东西。最短路径树有根且有向；最小生成树是无根且无向的。最短路径树是为有向图自然定义的；最小生成树是为无向图自然定义的。如果边权不同，只会存在一棵最小生成树，但是每个顶点都可以引导一棵不同的最短路径树；此外，有可能每个最短路径树会用到不同的最小生成树边的子集。

负权边

对于大多数最短路径问题，边对应着距离、长度或者时间，通常可以假设所有的边权值都是非负的，甚至是正的。然而对于许多最短路径算法的应用来说，也可以认为边权值是负的。比如，一条边的权值可能代表从一个点移动到另一个点的代价，所以负权边表示带有负代价的转变，或者同样地，这种转变可以获得利益。
　　负权边是最短路径问题的肉中刺，因为一个负权环的存在可能会导致最短路径的定义不明确。为了更明确，一条从s到t的最短路径存在当且仅当从s到t的路径存在，且s到t的路径中不存在负权环。对于任意带有负权环的路径，s到t的最短路径可以再通过一次负权环变得更短。这样，如果如果s到t的路径中存在一条带有负权环，那么s到t就没有最短路径。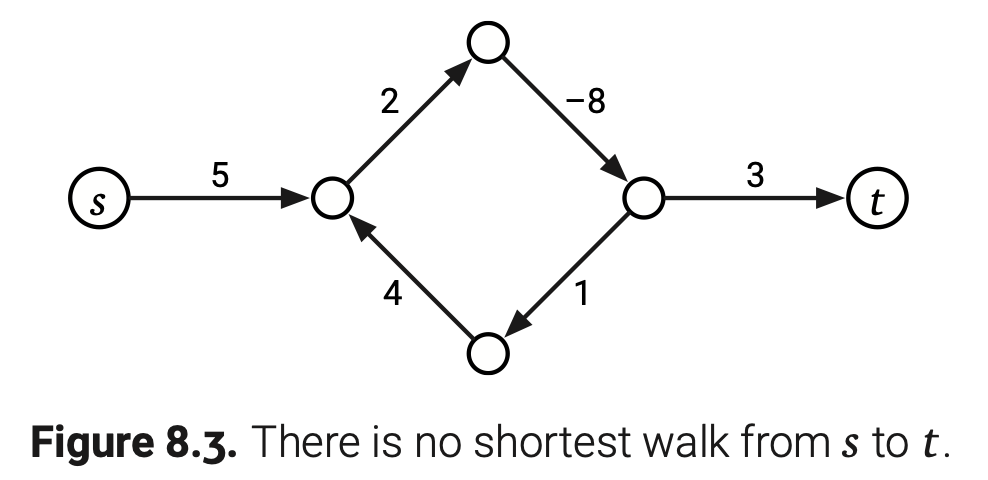

　　在某种程度上因为我们需要考虑负权边，本章明确只讨论有向图。所有本章描述的算法也可以用于无向图，只需一些大体上的细节改动，并且禁止存在负权边。正确地处理无向图中的负权边是非常巧妙的。我们不能简单的将一些有向边替换为无向边，因为这样会将负权边变成一个短的负权环。无向最短路径的子路径如果包含了负权边就一定不是最短路径；因此即使最短路径都是唯一的，一个单源点的所有最短路径组合起来可能不是一棵树。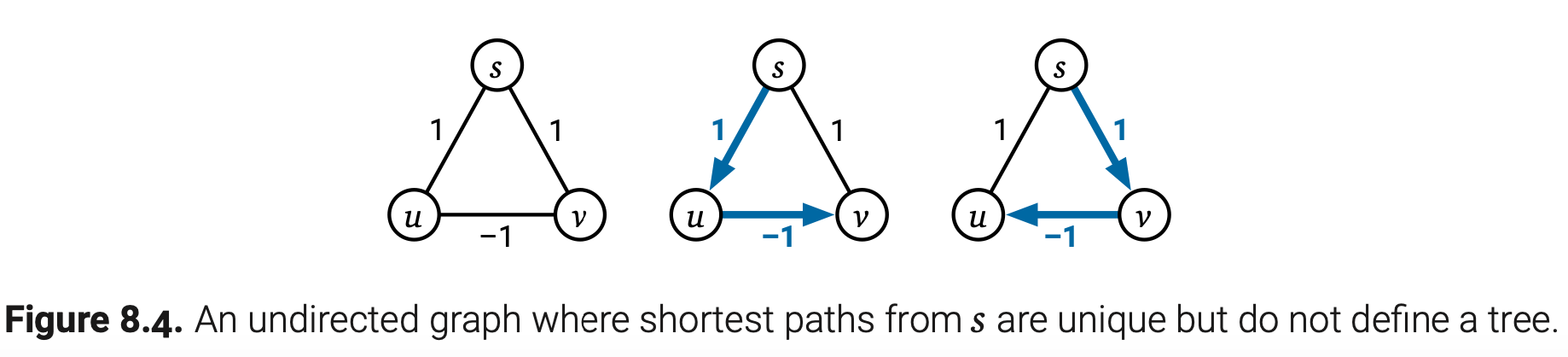

　　负权无向图的完整解决方案已经超出本书的范围。对于有些想要通过谷歌详细了解的人，我可以提醒一下负权无向图的单源最短路径通过约化最大权匹配的计算时间为$O(VE+V^2log V)$。

唯一的SSSP算法

就像图遍历和最小生成树一样，许多不同的SSSP算法可以被描述为一个单源泛型算法的实例，1956年Lester Ford首次提出了这个算法，接着又有一些人陆续二次发现。图中的每个顶点v存储了两个值，它们归纳地描述了一条从s到v的暂定最短路径。
　　• dist(v)是暂定最短路径$s\rightsquigarrow v$的长度，或者如果不存在路径则为$∞$
　　• pred(V)是暂定最短路径$s\rightsquigarrow v$中v的前驱顶点，或者如果不存在前驱则为Null。
前驱指针自动地定义了一棵根节点为s的暂定最短路径树；这些指针和我们通用图遍历算法的父指针是一样的。在算法开始阶段，我们初始化距离和前驱指针如下：

在算法执行过程中，如果dist(u)+w(u→v)＜dist(v)则边u→v是紧的（tense）。如果u→v是紧的，暂定最短路径$s\rightsquigarrow v$显然就是不正确的，因为$s\rightsquigarrow u\rightarrow v$更短。我们可以放松（relaxing）加入这条边来纠正错误：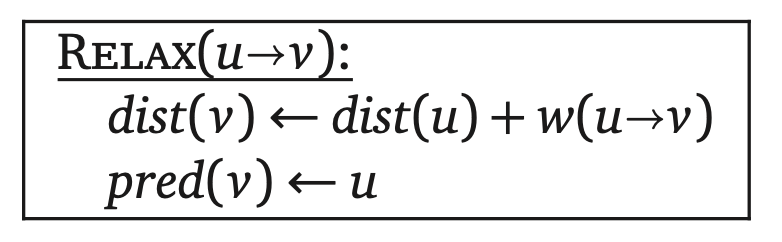

　　现在已经万事俱备了，Ford的泛型算法有一句简单描述：重复放松替换紧边，直到没有紧边存在。

如果FordSSSP因为没有紧边最终结束了，那么所有找到的这些前驱指针正好定义了一棵最短路径树，每个dist(v)的值就是从s到v的最短路径距离。特别注意，如果s不能到达v，那么dist(v)=∞，并且如果存在任意从s出发可达的负权环，那么这个算法将不会结束。
　　Ford泛型算法的正确性出自于以下一系列的简单声明：
　　1.在算法执行的任意时间段，对于每个顶点v，距离dist(v)不是∞就是一条从s到v的通路的长度。通过基于放松操作执行次数的归纳可以证明这个声明。
　　2.如果输入图不存在负权环，dist(v)不是无穷大就是某条从s到v的简单路径长度。尤其是，如果dist(v)是s到v的通路包含了有向环的长度，这个环一定有负权边。这个声明表示如果G没有负权环，放松算法最终会结束，因为G中简单路径的数量是有限的。
　　3.如果G中没有紧边，距离dist(v)就是前驱路径s→···pred(pred(v))→pred(v)→v的长度。尤其是，如果v违反了这个条件但是它的前驱pred(v)没有，那么pred(v)→v是一条紧边。
　　4.如果G中没有紧边，那么对于每个顶点v，前驱路径s→···pred(pred(v))→pred(v)→v事实上就是一条从s到v的最短路径。特别是，如果v违反了这个条件但在某个最短路径中它的前驱u没有，那么边u→v是一条紧边。这个声明表示如果G有负权环，那么有一些边永远都是紧的，所以泛型算法不会停止。
目前为止我们还没有讲怎么找到紧边，或者多条紧边存在的情况下应该使用哪一条。正如我们的任意优先搜索，Ford泛型算法存在多种不同的实例。然而与之不同的是，每个搜索策略的效率和正确性取决于输入图的结构。
　　剩下的章节我们会讨论四个常用的Ford算法实例，每一个都是相应输入图的最佳选择。

无权图：广度优先搜索

在最简单的最短路径的特殊案例中，每条边的权重都是1，路径的长度就是边的数量。这种特殊案例可以使用我们泛型图遍历算法中的广度优先搜索来解决。
　　广度优先搜索维护了一个顶点的先进先出队列，起初它里面只有一个源点s。在每次迭代中，算法拉出队列最靠前的顶点u并且检测它的每条出边u→v。无论何时算法发现一条出边u→v是紧的，他就会放松加入这条边并且将顶点v推入队列。算法在队列为空时结束。

　　如果我们将广度优先搜索的执行过程划分阶段（这里我们引入一个神奇的token），分析起来将会非常简单。在我们拉取任意顶点之前，我们将token推入队列。当我们拉取出来的是token时就表示当前阶段结束了；当再次我们将token推入队列是则表示下一个阶段开始了。这样，第一个阶段就是完全由源点s的搜索组成。这个算法在队列中只剩token时结束，修改后的算法如下图。

　　这里有必要强调一下，此改动只是为了方便分析；有没有token的存在，算法拉出和推入顶点的顺序是一样的，遍历边的顺序相同，输出的距离和前驱也是相同的。下图是这个算法的执行过程。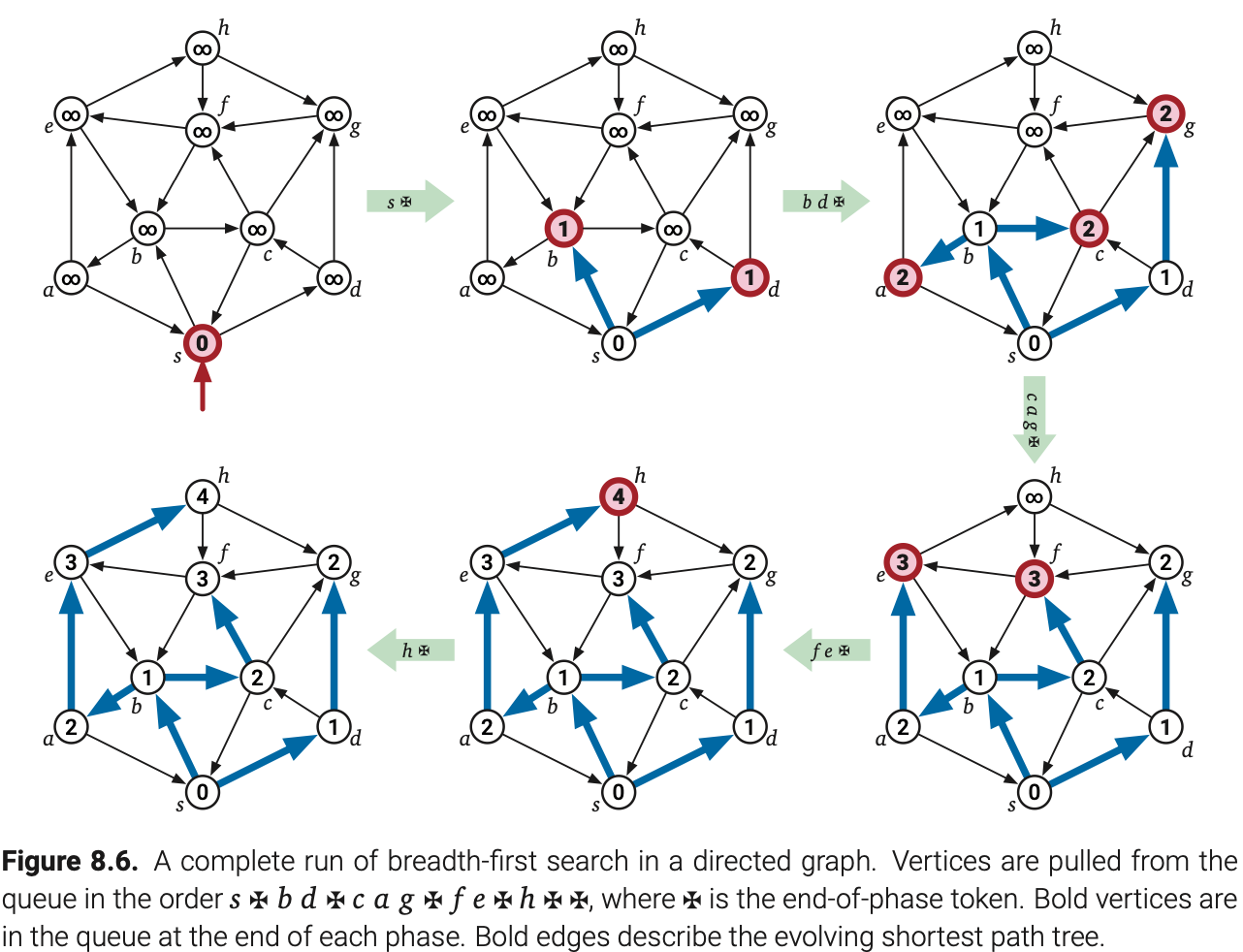

　　注意接下来这个引理，dist(v)只是一个算法维护的变量。尽管dist(v)直观上代表一条暂定最短路径的长度，我们不能确定dist(v)等于过s到v的真实最短路径的长度。别担心，我们会搞清这个问题的。

引理8.1. 对于每个整数i ≥ 0和每个顶点v，在第i阶段结束时，要么dist(v) = ∞，否则dist(v) ≤ i，v在队列中当且仅当dist(v) = i。

证明： 证明是基于对i的归纳，基础情况i=0：第1阶段开始（第0阶段结束），队列中只包含了一个起点s和token$✠$，并且InitSSSP方法设置了dist(s)←0和dist(v)←∞（所有v≠s）。
　　假设整数i＞0。归纳假设表明在第i阶段开始时，队列中包含了每个顶点u有dist(u)=i-1，最后跟着一个token$✠$。队列看起来是这样的：

$\overline{\underline{\rightarrow\ \ ✠\ \ \ i-1\ \ \ i-1\ \ ···\ \ i-1\ \ \rightarrow}}$

这样，在我们拉出token$✠$之前，我们会查看每条出边u→v。如果u→v是紧边，我们就会设置dist(v)←dist(u)+1，所以dist(v)=i，然后马上将v推入队列。这是在第i阶段中唯一的距离标记分配。通过归纳，在整个第i阶段中，队列包含着一些距离标记为i-1的顶点，往后是token，再接着是一些距离标记为i的顶点：

$\overline{\underline{\rightarrow \ \ i\ \ ···\ \ i\ \ \ \ ✠\ \ \ i-1\ \ ···\ \ i-1\ \ \rightarrow}}$

特别是，在第i阶段结束之前，队列中任然包含有token，后面是一些距离标记为i的顶点。

$\overline{\underline{\rightarrow\ \ \ i\ \ \ i\ \ ···\ \ i\ \ \ ✠\ \ \rightarrow}}$

此外，顶点v出现在最后这个队列中当且仅当dist(v)在第i阶段中改变了。这样，在第i阶段结束时，队列中包含的每个顶点v有dist(v)=i。

　　引理8.1表明BFS中标记距离是以非递减顺序；另外，每个顶点的dist(v)永远不会增加。也就是对于每个顶点v，在dist(v)阶段dist(v)←dist(u)+1这个操作最多执行一次，相似地：
　　• 在dist(v)阶段，每个前驱指针pred(v)最多改变一次。
　　• 在dist(v)阶段，每个顶点v最多被推入队列一次。
　　• 在dist(u)+1阶段，每个顶点u最多被拉出队列一次。
　　• 在dist(u)+1阶段，对于每条边u→v，比较“if dist(v)＞dist(u)+1”最多执行一次。
总体看来，这些观察表明广度优先搜索的执行是时间为$O(V+E)$。直观地，我们可以认为队列中的顶点的加入就像是从源点s开始的波扩散一样，经过图中的每个顶点和边最多一次。
　　这些观察也表明我们可以将条件“if dist(v)＞dist(u)+1”简化为“if dist(v) = ∞”。那么这里的距离和图遍历算法中维护的标记是一样的角色，都是保证每个顶点只访问一次。尤其是，一个顶点被标记当且仅当它的距离标签是有限的。
　但是我们仍然需要证明最终的距离标签是正确的！

定理8.2. 当BFS结束时，对于每个顶点v，dist(v)是G中从s到v的最短路径长度。

证明： 假设一个任意顶点v，G
中有一条任意路径$v_0\rightarrow v_1\rightarrow ···\rightarrow v_l$，$v_0=s$和$v_l=v$。我宣布对于每个索引j有$dist(v_j)\leq j$；特别是$dist(v)≤l$。我们通过对j的归纳来证明它。
　　• $dist(v_0)=dist(s)=0$
　　• 对于每个索引j＞0，由归纳假设可知$dist(v_{j-1})\leq j-1$。在我们将顶点$v_{j-1}$从队列中拉出时，要么$dist(v_j)\leq dist(v_{j-1})+1$，否则我们设置$dist(v_j)\rightarrow dist(v_{j-1})+1$。无论哪种情况我们都有$dist(v_j)\leq dist(v_{j-1})+1\leq j$。
我们已经证明了dist(v)不会超过从s到v的任意路径长度；也就是说dist(v)不会超过从s到v的最短路径的长度。
　　一个相似的归纳表明dist(v)是前驱路径s→···pred(pred(v))→pred(v)→v的长度，所以这一定是最短路径。

有向无环图：深度优先搜索

即使边是带权的，有向无环图的最短路径计算也是很简单的，尤其是，带有负权边。（我们不需要担心负权环，因为根据定义已经排除了）甚至，这就是一个完全标准的动态规划算法。
　　G是一个带负权边的有向图，s是一个任意的起点。对于任意顶点v，dist(v)表示G中从s到v的最短路径长度。这个函数满足一个简单的递推式：

$\begin{equation}dist(v)=\begin{cases}0 & if\ v=s\\ \min\limits_{u\rightarrow v}(dist(u)+w(u\rightarrow v)) & otherwise\end{cases}\end{equation}$

事实上，这个特性适用于所有的有向图，但是这个递推式只适用于有向无环图。如果输入图G包含一个环，那么这个函数的递归计算将会进入一个无限循环；然而，因为G是有向无环图，每个递归调用都是访问拓扑顺序中前面的顶点。
　　这个递推式的依赖图就是输入图G的反转图：子问题dist(v)依赖于dist(u)当且仅当u→v是G中的一条边。这样，我们以后序排列在反转图G中执行深度优先搜索计算距离的时间是O(V+E)。同样地，我们这样做就等于在原图中以拓扑顺序遍历顶点，代码如下：

　　最终的动态规划算法就是另一个Ford泛型算法的实例！为了让这部分内容的连接更清晰，我们可以将dist(v)的初始化移到主循环外面并且增加一个前驱指针计算，改动如下：

下图展示了算法的操作过程：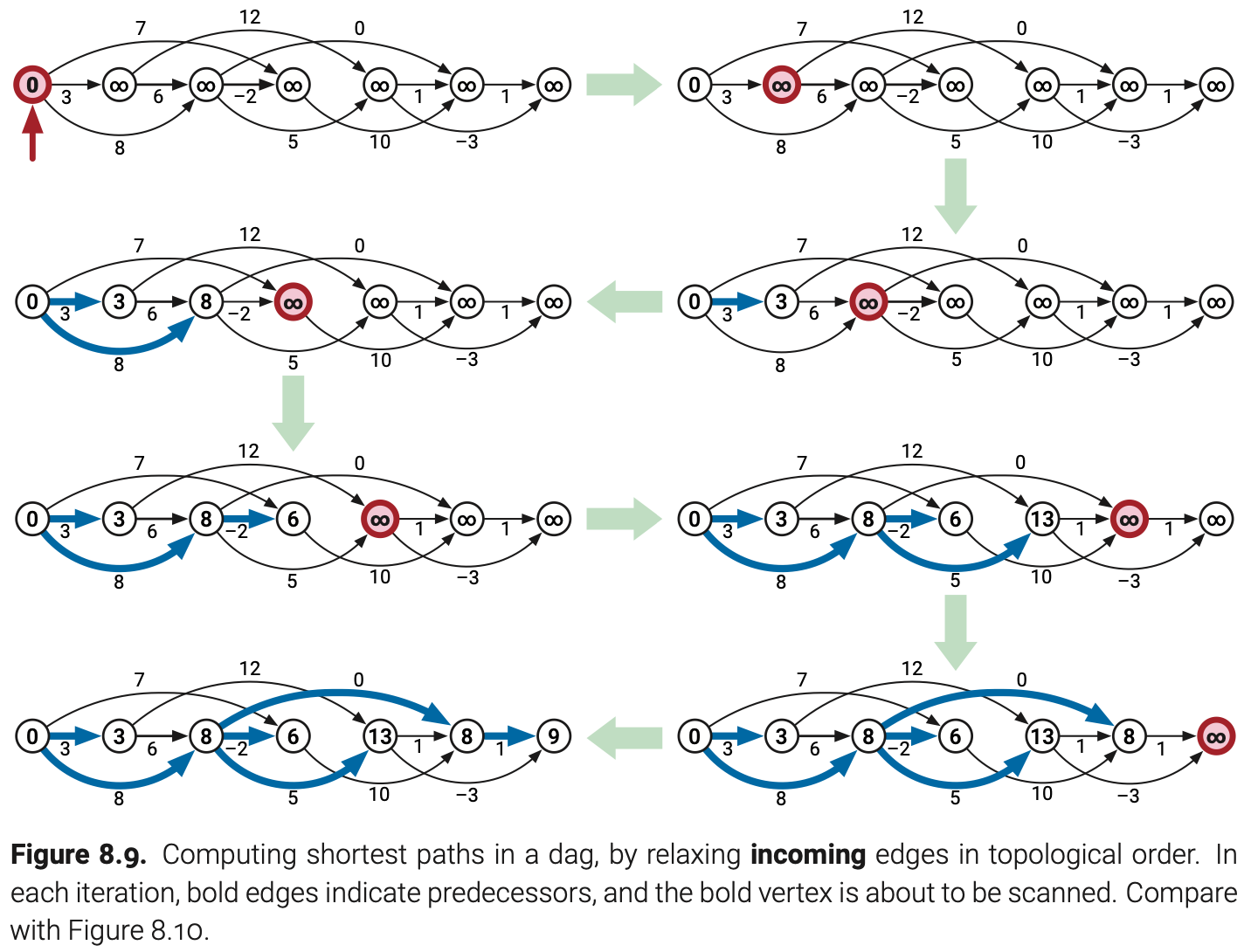

　　DagSSSP与广度优先搜索及其他Ford的放松策略有一个细微方面的不同。无论何时这些其他的算法访问一个顶点，它们都试图放松它的每一条出边，直观上看就是从源点开始往外的波扩散；然而，DagSSSP则尝试放松每个顶点的入边，直观上开来就是一个往内的波扩散。
　　不过，如果我们修改DagSSSP为放松出边，就得到了另一个在O(V+E)时间内计算有向无环图最短路径的算法，而且也更类似于我们其他的最短路径算法。

下图是修改后算法的操作过程：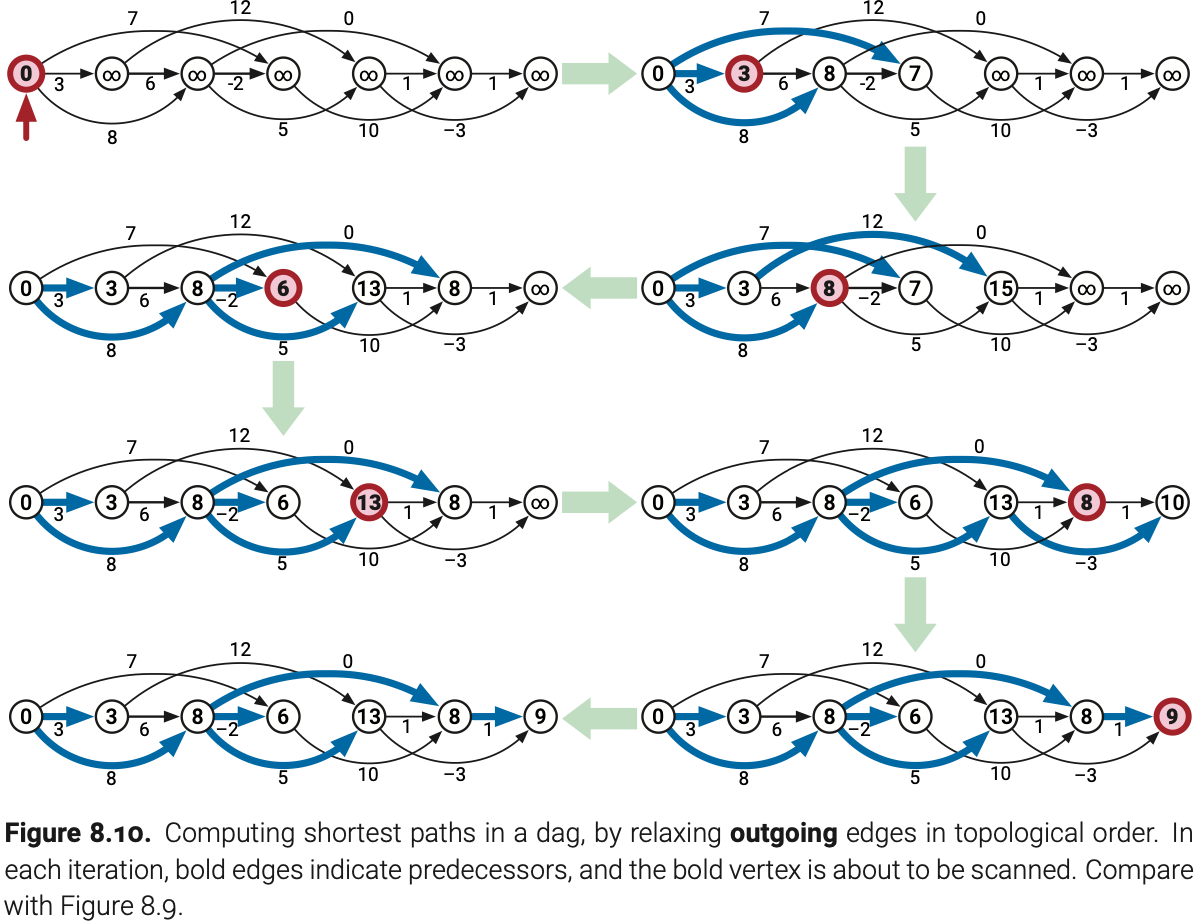

PushDagSSSP的正确性源于Ford的放松策略，但是直接证明也不困难，基于拓扑顺序归纳即可。

最佳优先：Dijkstra算法

如果我们将广度优先搜索中的FIFO队列改成优先队列，优先级是根据那个顶点的暂存距离最小，我们就得到了另一个广为人知的算法。伪代码如下：

　　一个简单的归纳表明，在这个算法的执行时间内，一条边u→v是紧边当且仅当顶点u在优先队列中或者u刚从优先队列中被取出。这样，Dijkstra算法也是一个Ford通用策略的实例，这表明它可以正确计算出最短路径，当然输入图G中不能包含负权换。

无负权边

Dijkstra算法在输入图无负权边的情况下是能正常运行的。在这个条件下，算法直观上是一个从源点开始的波扩散，根据到s的距离递增遍历顶点，和广度优先搜索类似。下图是算法的操作过程：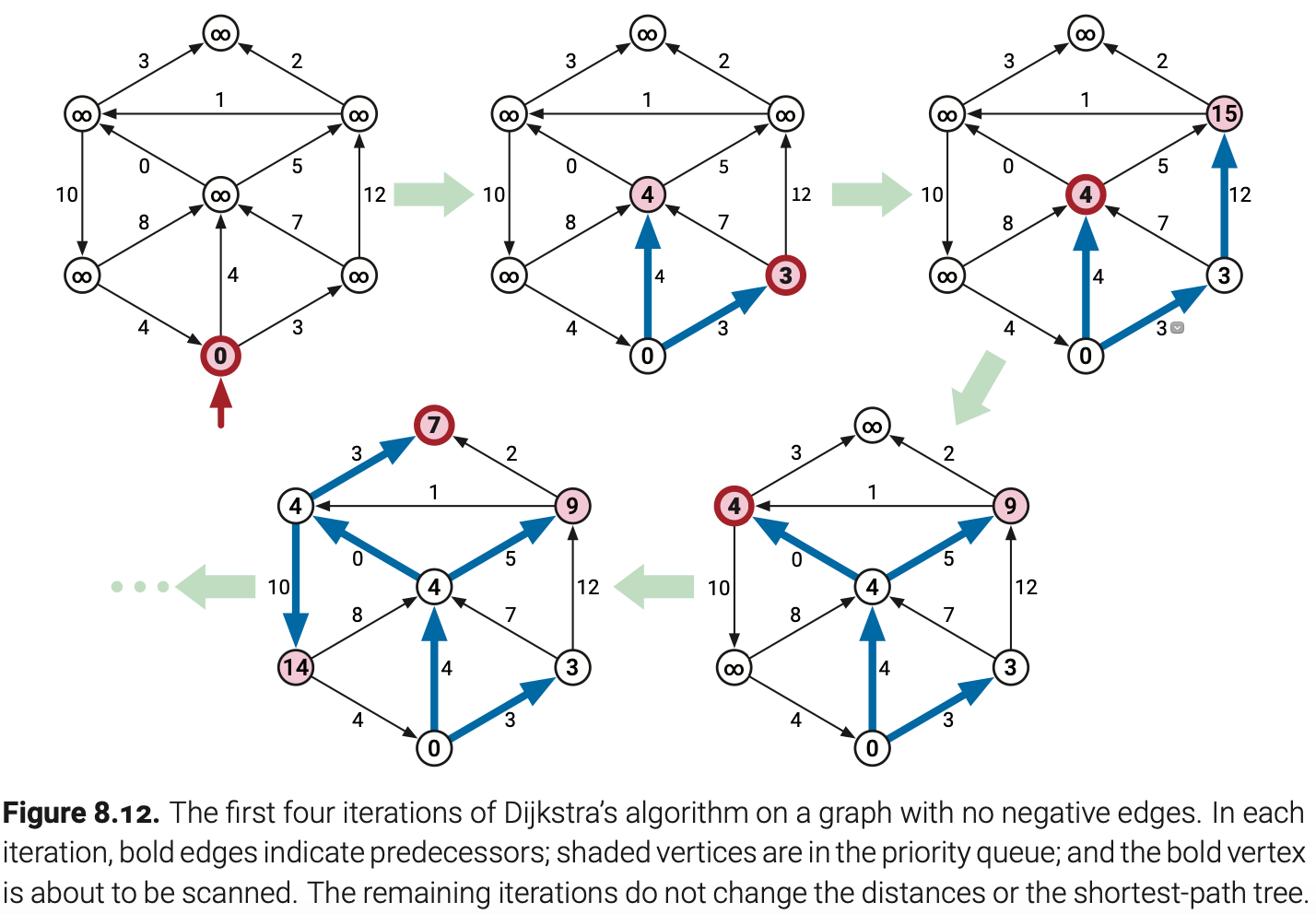

　　在这种条件下，我们可以形式化这种波扩散得出Dijkstra算法正确性的完备证明。对于每个整数i，用$u_i$表示第i次调用ExtractMin返回的顶点，用$d_i$表示Extraction操作后$dist(u_i)$的值。特别是，我们有$u_1=s$和$d_1=0$。我们不能假设这种情况下$u_i$是不同的；因为一个顶点可能被取出多次。

引理8.3. 如果G没有负权边，对于所有i＜j，有$d_i\leq d_j$。

证明： 假设G没有负权边，已知任意索引i；为了证明这个引理，我们先证明$d_{i+1}\geq d_i$。这里有两种情况需要考虑。
　　• 如果G包含了边$u_i\rightarrow u_{i+1}$，并且这条边在主循环第i次迭代中被放松加入了，那么在第i次迭代结束时，我们有$dist(u_{i+1})=dist(u_i)+w(u_i\rightarrow u_{i+1})\geq dist(u_i)$。
　　• 否则，在第i次迭代开始之前，$u_{i+1}$一定早已在优先队列中，而且由于优先级关系，有$dist(u_{i+1})\geq dist(u_i)$。此外，$dist(u_{i+1})$在第i次迭代过程中没有改变。
在两种情况下，我们都得出$d_{i+1}\geq d_i$，现在通过对i进行归纳即可证明引理。

引理8.4. 如果G没有负权边，G中的顶点从优先队列中被取出最多一次。

证明： 假设v被取出超过一次。特别地，假设v在主循环第i次迭代中被取出，在第j次迭代中被插入，并且在第k次迭代中被再次取出，对于这些索引i < j < k。根据前面的设定，有$v=u_i=u_k$。
距离标签dist(v)永远不会增加。甚至，dist(v)在第j次迭代中被插入之前还降低了。也就是说$d_i>d_k$。因此，根据前一个引理，G至少包含了一条负权边。

　　引理8.4表明每个顶点最多被取出一次，也就是每条边最多被放松一次。然而，不像广度优先搜索，每个距离标签dist(v)能改变多次。第一次我们将顶点v插入优先队列，dist(v)由∞发生变化；之后，每次dist(v)改变都是由于DecreaseKey被调用。在v从优先队列中被取出后，它的距离标签就不会变化了。
　　剩下的正确性证明和广度优先搜索的几乎一样。

定理8.5. 如果G没有负权边，那么当Dijkstra算法结束时，对于每个顶点v，dist(v)就是G中从s到v的最短路径长度。

证明： 假设一个任意顶点v，G中存在一条任意路径$v_0\rightarrow v_1\rightarrow ···\rightarrow v_l$，且$v_0=s$和$v_l=v$。对于任意顶点j，用$L_j$表示子路径$v_0\rightarrow v_1\rightarrow ···\rightarrow v_j$的长度。我们通过归纳证明对于所有的j有$dist(v_j)\leq L_j$。
　　• $dist(v_0)=dist(s)=0=L_0$
　　• 对于任意索引 j＜0，归纳假设表明$dist(v_{j-1})\leq L_{j-1}$。当我们从队列中取出顶点$v_{j-1}$时，要么$dist(v_j)\leq dist(v_{j-1})+w(v_{j-1}\rightarrow v_j)$，否则我们就会设置$dist(v_j)\leftarrow dist(v_{j-1})+w(v_{j-1}\rightarrow v_j)$。无论哪种情况，我们都有

$dist(v_j)\leq dist(v_{j-1})+w(v_{j-1}\rightarrow v_j)\leq L_{j-1}+w(v_{j-1}\rightarrow v_j)=L_j$

我们刚刚证明了dist(v)不会超过任意从s到v的路径长度；也就是说dist(v)不会超过最短路径的长度。
　　另外，相似的归纳法可以证明dist(v)就是前驱路径s→···→pred(pred(v))→pred(v)→v的长度。

　　接下来就是要确定算法的时间界限。总的算下来Dijkstra算法执行了最多E次DecreaseKey操作，最多V次Insert和ExtractMin操作。这样，如果我们采用标准二进制堆的优先队列，它支持每种操作的时间为O(log V)，Dijkstra算法的运行时为O(Elog V)。
　　如果我们提前知道输入图不会包含负权边，我们可以稍微简化一下Dijkstra算法，通过直接在初始化阶段将每个顶点插入优先队列，只在主循环中调用DecreaseKey。改动如下：

大多数算法书、维基百科级Dijkstra的原稿中提到的都是这个版本的算法；这也是第五章提到过的最佳优先搜索的例子。

负权边

然而，NonnegativeDijkstra不能正确计算负权图中的最短路径。此外，当所有边的权值都是正的，NonnegativeDijkstra也不必Dijkstra快（不管理论还是实践）。因为这两方面的原因，相较于NonnegativeDijkstra，Dijkstra更值得被称为Dijkstra算法。即便是Edsger Dijkstra也会同意较慢的正确的算法比较快的不稳定算法更好！
　　不幸的是，当输入图有负权边时，常见的波扩展方式将不再精确了。同一个顶点会被取出多次；同一条边会被放松多次；而且距离标记不会以递增顺序被发现。下图的例子中左上方的顶点被取出了六次，上方的三条边各被放松了两次。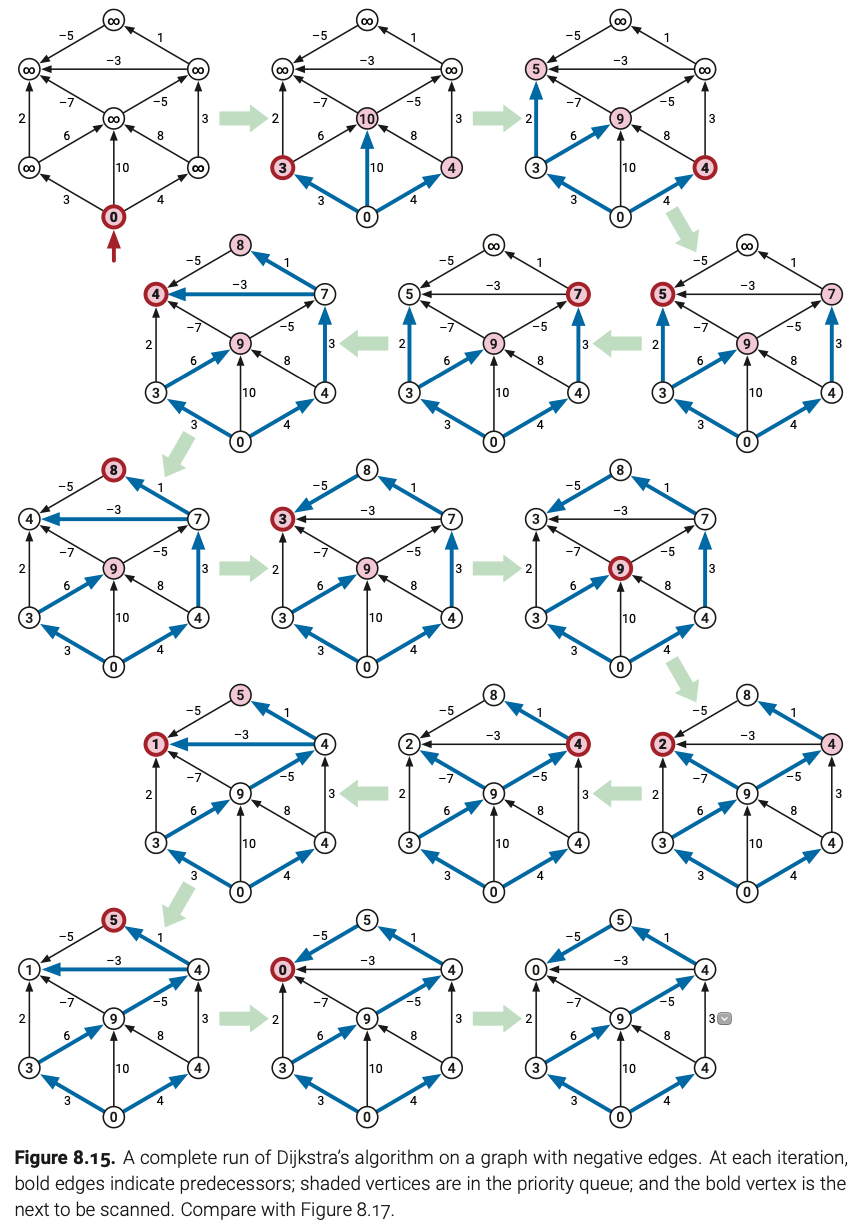

　　对于无负权环但不限制负权边的图，Dijkstra算法的最坏运行时实际上是指数级的。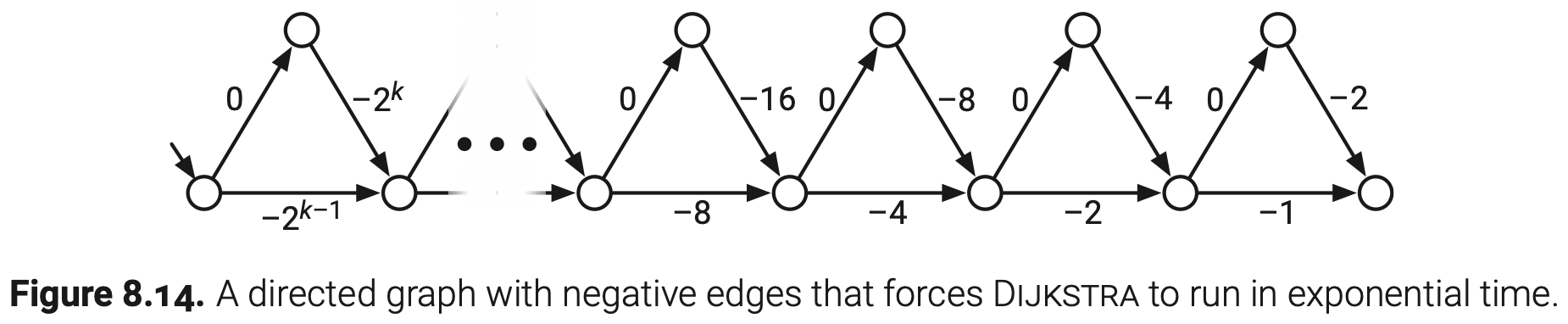

上图中的输入图迫使Dijkstra执行$\Theta(2^{V/2})$次放松（这里我自己算出来V/3…）。还有更复杂的图可以迫使算法执行$\Theta(2^{V})$放松，这也是最坏的可能情况。然而实际上Dijkstra算法对于负权图通常还是比较快的。

放松所有边：Bellman-Ford算法

Bellman-Ford算法总结下来就是一句话：放松当前所有的紧边，然后递归。

　　接下来的引理是证明Bellman-Ford算法正确性和效率的关键。对于每个顶点v和非负整数i，用$dist_{\leq i}(v)$表示G中从s到v不超过i条边的最短通路长度。特别是，$dist_{\leq 0}(s)=0$以及对于所有v≠s有$dist_{\leq 0}(v)=∞$。

引理8.6. 对于每个顶点v和非负整数i，在BellmanFord的主循环的第i次迭代，我们有$dist(v)\leq dist_{\leq i}(v)$。

证明： 证明基于对i的归纳，基础情况下i=0就不分析了，所以假设i＞0。已知一个顶点v，用W表示从s到v不超过i条边的最短通路。根据定义，W的长度是$dist_{\leq i}(v)$。这里我们需要考虑两种情况。
　　• 假设W没有边。那么W一定是从s到s的通路，所以v=s并且$dist_{\leq i}=0$。我们初始化设置dist(s)←0，而且dist(s)不会增加，所以我们有dist(s)≤0。
　　• 否则，让u→v左右W的最后一条边。归纳假设表明在第i-1次迭代后，$dist(u)\leq dist_{\leq i-1}(u)$。在外层循环的第i次迭代，当我们在内层循环中遍历到边u→v，要么已经有$dist(v)<dist(u)+w(u\rightarrow v)$，否则我们将设置$dist(v)\leftarrow dist(u)+w(u\rightarrow v)$。两种情况下，我们都得出$dist(v)\leq dist_{\leq i-1}(u)+w(u\rightarrow v)=dist_{\leq i}(v)$。照例，dist(v)不会增加。
由此，我们得出在第i次迭代结束时$dist(v)\leq dist_{\leq i}(v)$。

　　如果输入图中没有负权环，从s到任意顶点的最短通路应该是一条不超过V-1条边的简单路径；也就是说Bellman-Ford算法应该在第V-1次迭代后停止得到正确的最短路径。换句话说，如果任意边在V-1次迭代后任然是紧的，那么输入图一定包含了负权环！这样，我们将算法改改得更具体些：

　　每次内层循环的执行次数最多为O(E)，所以总的来说算法的运行时为O(VE)。这样，即使图中包含负权边Bellman-Ford算法也总是高效的，甚至有负权环也是如此。
　　如果所有的边权都是非负的，就最坏情况来说Dijkstra算法是最快的。（实际上，Dijkstra算法在有负权边的情况下也经常快于Bellman-Ford算法）

Moore的改进

Moore的算法和Bellman-Ford本质上是一样的。虽然它们具有相同的最坏运行时O(VE)，但是在实践中Moore算法更快，直观上是因为它避免了检查明显不紧的边。
　　Moore基于对广度优先搜索的两处改动得出它的加权最短路径算法。首先，将最内层循环的每个“+1”改成“+w(u→v)”，确保每个边的权值加入计算。其次，检测顶点在插入前是否已在FIFO队列中，所以队列中每个顶点只保存一份。
　　根据我们早期对广度优先搜索的分析，我们用“token”✠将整个算法的执行过程分阶段。和广度优先搜索一样，一个阶段在token被推入时开始，在token被拉出时结束。同样，队列中只有token时算法结束。算法如下图所示：

　　因为在任何时候队列中一个顶点只能同时存在一份，每个顶点在每个阶段最多被拉出一次，每条边u→v在每个阶段最多被检测一次是否为紧边。此外，每条在阶段开始时是紧的边都会在这个阶段被放松。（一些边可能在阶段中变紧后被放松，一些边被放松的边可能又会变紧）这样，Moore算法可以被看做是改进后使用队列维护紧边的BellManFord，而不是暴力测试每条边是不是紧边。特别是，一个相似的归纳证明可以建立类似于引理8.6的理论：

引理8.7. 对于每个顶点v和非负整数i，在Moore算法第i阶段后，有$dist(v)\leq dist_{\leq i}(v)$。

　　这样，如果输入图没有负权环，Moore最多执行V-1个阶段就会停止。在每个阶段，我们访问每个顶点最多一次，所以我们最多放松每条边一次，所以单个阶段的最坏运行时是O(E)。这样，总的算来Moore的运行时是O(VE)。然而实际上，Moore计算最短路径快过BellmanFord很多，因为只有在上个阶段dist(u)发生变化当前阶段才会访问边u→v。
　　如果输入图中有负权环，Moore则不会结束。不过，我们可以像BellmanFord算法一样记录阶段数量。或许最早的这种改动就是维护一个token，计算从队列中拉出token的次数。那么输入图存在负权环当且仅当第V-1次拉出token时队列不为空。

动态规划形式

Richard Bellman是通过动态规划得出算法的。照例，我们需要给出一个最短路径距离的递归定义。直接使用有向无环图的递推式是相当有诱惑力的：

$\begin{equation}dist(v)=\begin{cases}0 & if\ v=s\\ \min\limits_{u\rightarrow v}(dist(u)+w(u\rightarrow v)) & otherwise\end{cases}\end{equation}$

不过如果输入图不是有向无环图，这个递推式就不起作用了！假设输入图有个有向环u→v→w→u。计算dist(w)我们需要知道dist(v)，计算dist(v)我们需要知道dist(u)，但是计算dist(u)我们需要知道dist(w)。如果输入图有任何有向环，我们就会陷入无限循环！
　　为了提供一正确的递推式，我们需要在距离函数中添加额外的结构参数，它会在每次递归调用后自动减少，这样定义当参数变为0时函数计算就结束了，Bellman选择最大边数量作为额外参数。
　　正如我们早期的分析，用$dist_{\leq i}(v)$表示从s到v不超过i条边的最短通路长度。Bellman观察到这个函数遵循以下递推式：

$\begin{equation}dist_{\leq i}(v)=\begin{cases}0 & if\ i=0\ and\ v=s\\∞ & if\ i≠0\ and\ v=s\\ min\begin{cases}dist_{\leq i-1}(v)\\ \min\limits_{u\rightarrow v}(dist_{\leq i-1}(u)+w(u\rightarrow v))\end{cases}& otherwise\end{cases}\end{equation}$

　　我们假设输入图没有负权环，所以我们的目标是计算出每个顶点的$dist_{\leq V-1}(v)$。现在有一个使用此递推式简单动态规划算法，$dits[i,v]$存储的是$dist_{i}(v)$的值。最终最短路径距离的正确性取决于这个递推式，明显它的运行时是O(VE)。具体算法代码如下：

　　通过一系列简单的操作我们可以将这个动态规划算法转变成原始形式的BellmanFord。首先，最外层循环的每次迭代访问每条边最多一次，而且我们访问这些边的顺序也不重要。这样，我们可以安全的最后三步提出当前循环！改动后的算法遍历边的顺序不同了，但是对于所有的i和v它依然能正确计算$dist_{\leq i}(v)$。

　　接下来我们将最后两步的索引i-1改成i。这个改动也许会让$dist[i,v]$比以前更快接近真实的最短路径距离。对应引理8.6和8.7，我们现在有$dist[i,v]\leq dist_{\leq i}(v)$，而不是$dist[i,v]=dist_{\leq i}(v)$。

　　但是这个算法看起来有点蠢，在最外层循环的第i次迭代中，我们将数组dist[·,·]的第i-1行复制给了第i行，然后又开始修改第i行的每个元素。所以我们根本不需要一个二维数组；索引i完全就是冗余的！在我们最终改版里，我们只需要维护一个一维的暂存距离数组。

　　这个最终版本的动态规划算法就和我们BellmanFord的原始形式一样了！开始的三行就是初始化最短路径距离，最后的两行就是当边是紧的就放松加入。BellmanFordFinal与我们的原始形式有两个不同特征：没有维护前驱指针和没检测负权环。