前言
这个问题单独讲了一篇,必定有其中的奥妙。目前为止图类算法的最优运行时应该是O(VE)级别的,如果算法存在重复遍历点和边那就可能还存在可优化的地方,所以单纯使用单源最短路径算法解决此问题并不是最优解。当然这是我个人的感觉,话先撂这儿,等被打脸再说。👀
知识点
在前一章中我们讨论过几个单源最短路径算法,已知图中一个起点s,计算出它到图中其他顶点的最短路径。
• dist(v)表示从s到v的最短路径长度;
• pred(v)表示从s到v的最短路径中的倒数第二个顶点。
在本章,我们考虑更普遍的完全最短路径问题,也就是每个可能的源点到图中所有顶点的最短路径。对于每对顶点u和v,我们想计算出一下信息:
• dist(u,v)表示从u到v的最短路径长度;
• pred(u,v)表示从s到v的最短路径中的倒数第二个顶点。
这些直观地定义不包含一些边界情况,所有这些我们在上一章中都见过。
• 如果从u到v没有通路,那么也就不存在从u到v的最短路径;这种情况下,我们定义dist(u,v)=∞以及pred(u,v)=Null。
• 如果u和v之间存在负权环,那么通过这个环可以缩减路径长度;这种情况下,我们定义dist(u,v)=-∞以及pred(u,v)=Null。
• 最后,如果u不在负权环中,那么从u到自身的最短路径不需要边,因此就没有上一条边;这种情况下,我们定义dist(u,u)=0以及pred(u,u)=Null。
完全最短路径问题的期望输出是一对V * V数组,一个存储$V^2$个最短路径距离,另一个存储$V^2$个前驱指针。在本章,我们更倾向于计算距离数组。至于前驱数组,我们可以对计算过程做一些小改动即可得到。
大量单一源点
完全最短路径问题最明显的解决方案就是执行V次单源最短路径算法,一个源点执行一次。特别地,为了填充一维子数组dist[s,·],我们对源点s调用单源最短路径算法。这种算法运行时取决于我们采用哪一种单源最短路径算法。根据图的结构和边权,这里我们有四种选择:
• 如果图是无权的,使用广度优先搜索的总运行时为$O(VE)=O(V^3)$。
• 如果图是有向无环的,使用拓扑顺序遍历顶点的总运行时为$O(VE)=O(V^3)$。
• 如果所有边权都是非负的,使用Dijkstra算法的总运行时为$O(VE logV)=O(V^3 logV)$。
• 最后,通常情况下使用Bellman-Ford算法的总运行时为$O(V^2E)=O(V^4)$
再赋权
负权边确实很影响我们的计算速度;但我们能摆脱它吗?如果每条边增加相同的值让所有的边权都变成正的,那么我们就可以用Dijkstra而不是Bellman-Ford算法,很多人都有过这样的注意。然而,这个简单的想法不行,因为直观上来说因为两种“长度”概念是矛盾的—边多的路径权值可能比边少的路径权值还小。如果我们以同样的速率增加边权,边多的路径将会边少的路径增长更快;这样,两个顶点之间的最短路径就可能发生变化。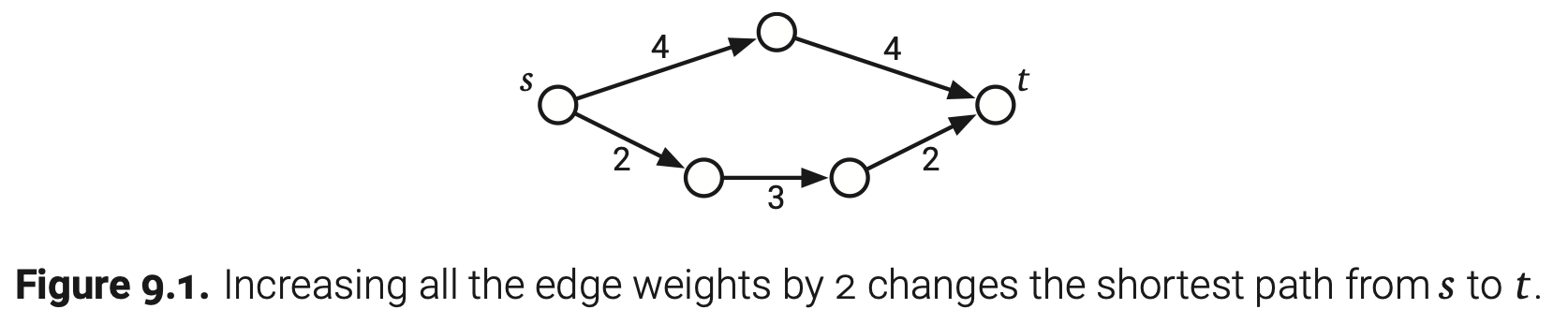
然而,确实存在一个非常微妙的再赋权方法,它可以保存最短路径。假设每个顶点一个关联代价$π(v)$,它可以是正数、负数或者0。我们可以定义一个新的权值函数:
$w’(u\rightarrow v)=\pi(u)+w(u\rightarrow v)-\pi(v)$
为了方便理解,想象一下当我们离开顶点u时,我们需要付一种退出税务$\pi(u)$,当我们进入顶点v时,我们得到一种加入收益$\pi(v)$。
不难发现新的权值函数$w’$和原权值方程$w$是一样的,实际上,对于任意从u到v的路径$u\rightsquigarrow v$,我们有
$w’(u\rightsquigarrow v)=\pi(u)+w(u\rightsquigarrow v)-\pi(v)$
我们付出$\pi(u)$的税务,加上原来路径的权值,减去$\pi(v)$的收益。至于路径中的每个中间顶点,我们得到$\pi(x)$的收益,但是又马上作为税务出去了!因为所有从u到v的路径长度改变的量是一样的,所以从u到v的最短路径没有改变。
Johnson算法
Johnson的完全最短路径算法计算出每个顶点的关联代价$\pi(v)$,所以每条边的新权值都是非负的,然后基于这些再赋权的边再使用Dijkstra算法。
首先,假设输入图有一个顶点s可以到达所有其他顶点。Johnson使用Bellman-Ford算法计算出从s到所有其他点的最短路径,然后在使用代价函数$\pi(v)=dist(s,v)$对图进行再赋权。每条边的新权值遵循以下函数:
$w’(u\rightarrow v)=dist(s,u)+w(u\rightarrow v)-dist(s,v)$
因为Bellman-Ford算法停止了,所以新的权重都是非负的!回想一下$u\rightarrow v$是紧边,仅当$dist(s,v)+w(u\rightarrow v)<dist(s,v)$,而且单源最短路径算法会排除所有的紧边。
如果不存在合适的顶点s,那么不管从哪里启动Bellman-Ford算法都会有一些顶点的代价是无穷大。为了避免这种情况,我们总是增加一个新顶点s到输入图中,它到所有其他顶点的边权为0,但是没有边可以到达s。这个改动不会改变原来任意两个点之间的最短路径,因为没有路径可以到达s。
完整的伪代码如上图所示。这个算法的运行时由调用Dijkstra的次数决定。尤其是,我们花费了O(VE)执行BellmanFord一次,O(VE logV)执行了V次Dijkstra,以及O(V+E)用来记账。这样,全部的运行时间就是$O(VE logV)=O(V^3logV)$。负权边也不能减慢我们的速度!
动态规划
我们也可以直接使用动态规划来解决完全最短路径问题,而不是多次调用单源算法。对于稠密图,有$E=\Omega(V^2)$,动态规划最终产出的算法相较于Johnson算法更快更简单。本章剩余部分,我们直接假设输入图不包含负权环。
通常对于动态规划算法,我们首先需要一个递推式。和单源算法一样,有“明显”的递归定义如下:
当然它只会在输入图为有向无环图时有效;任何有向环都会使这个递推式进入无限循环。
通过引入一个额外参数,我们可以打破这个无限循环,正如我们对Bellman-Ford算法所做的;用$dist(u,v,l)$表示从u到v经过最多l条边的最短路径长度。最短路径最多经过V-1条边,所以真正的最短路径距离就是$dist(u,v,V-1)$。Bellman的单源递推式采用这个设置后变成:
将这个递推式直接转化成动态规划算法;产出算法运行时为$O(V^2E)=O(V^4)$。
和Bellman-Ford算法的优化一样,我们不需要最内层的对于顶点v的循环和迭代索引l。改动后的算法如下。
从这个推导过程,不难看出这个产出算法和交错执行V次不同源点的Bellman-Ford算法一样。特别是,对于所有的顶点u和v,在主循环l次迭代后,$dist[u,v]$的值不会超过从u到v不超过l条边的最短路径长度。
分而治之
但是我们还有更进一步的改动。通过考虑目标顶点的所有可能前驱,Bellman的递推式将最短路径看作是一条更短的最短路径和一条边。相反,如果我们将最短路径看作是经过一些中间点的两条更短的最短路径。这个想法给了我们一个不同含义的的相同递推式$dist(u,v,l)$,这里我们基础情况是l=1而不是l=0,因为只有一条边的路径是没有中间点的。为了方便简化这个递推式,我们定义对于每个顶点v有$w(v\rightarrow v)=0$。
如你所见,在这个递推式中l必须是2的次方数,否则我们可能就要去寻找小数条边!但是这并不是什么大问题;如果$l\geq V-1$那么$dist(u,v,l)$就是从u到v的最短路径;特别是,我们可以用$l=2^{\lceil lgV\rceil}<2V$。(国内lg的底数是10,但是作者在此处想用的底数应该是2)
再一次,动态规划算法结构是很清晰的。即使我们没有写出算法,也能得出运行时$O(V^3logV)$—我们需要u、v和x各V个,以及$\lceil lgV\rceil$个不同l的值。在接下来的伪代码中我们用数组元素$dist[u,v,i]$存储$dist(u,v,2^i)$的值。
不像我们早期的算法,FischerMeyerAPSP与调用V次单源最短路径的算法不同;特别是,最内层的循环不是简单的放松紧边。不过,我们任然可以移除数组的最后一维,使用$dist[u,v]$替换每一处$dist[u,v,i]$,正如我们前面对动态规划算法的处理;这将空间复杂度从$O(V^3)$降到了$O(V^2)$。
趣味矩阵乘法
计算有向图的最短路径和计算矩阵的幂有非常紧密的关联。将FischerMeyerAPSP的内层循环和下面n*n矩阵平方的算法相比较。
两个算法的唯一不同点在于第二个算法使用加法代替乘法,取最小值代替加法。由于这个原因,最短路径的内层循环有时会被称为“趣味”矩阵乘法。
我们较慢的算法ShimbelAPSP就是对权重矩阵w计算V-1次“趣味”矩阵乘法的标准迭代算法。在设置循环中我们将矩阵的对角线都设成0,其余设成∞。在第二个主循环中我们使用上一次的结果继续执行“趣味”矩阵乘法。
目前存在很多处理矩阵乘法更快的分治算法,它们都极大的提升了运算时间。但是所有这些更快的算法都用到了减法,但是我们还不知道减法的“趣味”转换是什么。(取最小值的反操作是什么?)所以至少对于一般图来说,没有“明显”的方法可以优化动态规划算法的内层循环。
Floyd-Warshall(Kleene)算法
我们最快动态规划算法和标准Johnson算法都有一个因子$O(logV)$。Kleene发现了一种表述方式可以移除这个对数因子,他依然使用之前的动态规划递推式。但是第三个参数的含义却不同了,它不再是限制边的数量,而是一些可以通过的确定顶点。此处,“通过”是指“进入然后离开”;比如,路径$w\rightarrow x\rightarrow y\rightarrow z$从w开始通过x、y最终到达z。
用数字1到V来随意标记所有顶点。对于每对顶点u和v以及整数r,我们定义$\pi(u,v,r)$表示从u到v经过数字标记不超过r的顶点的最短路径。特别是,$\pi(u,v,V)$确实表示了从u到v的最短路径。我们观察到这些路径都有一个简单的递归结构。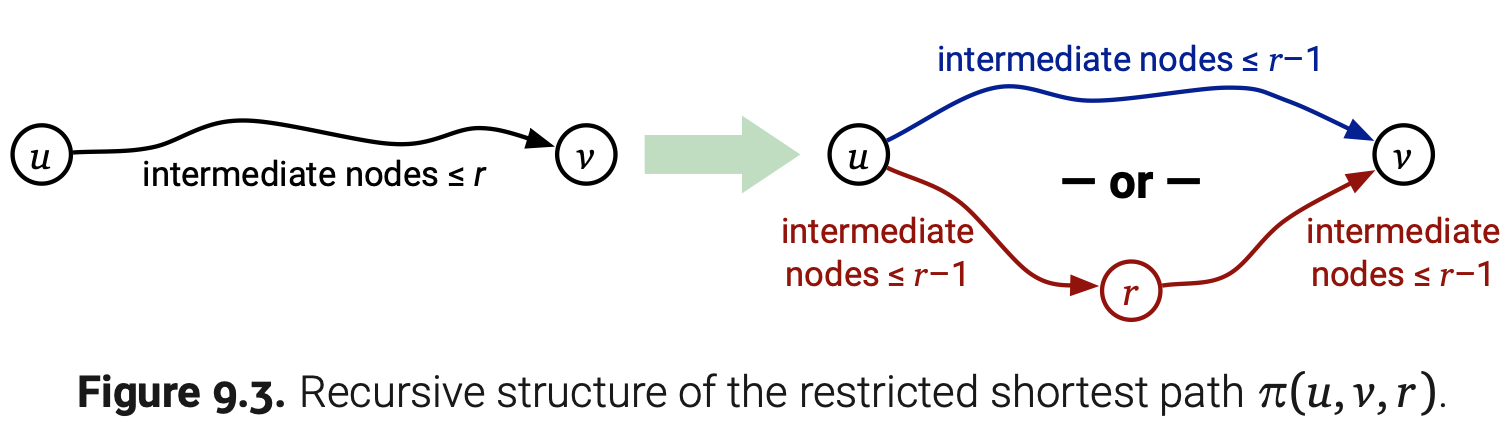
• 路径$\pi(u,v,0)$不通过任何中间点,所以它表示u到v这条边。
• 对于任意$r>0$,$\pi(u,v,r)$要么通过顶点r,要么不通过。
- 如果$\pi(u,v,r)$通过顶点r,那么它就由从u到r和从r到v的子路径构成。两条子路径经过的中间点的顶点标记不会超过r-1;此外,由于条件限制子路径也是最短的。所以两个子路径一定是某一对$\pi(u,r,r-1)$和$\pi(r,v,r-1)$。
- 另外,如果$\pi(u,v,r)$不通过顶点r,那么它通过的顶点标记不超过r-1,由于条件限制它一定是最短路径。所以在这种情况下,我们得到$\pi(u,v,r)=\pi(u,v,r-1)$。
现在用$dist(u,v,r)$表示路径$\pi(u,v,r)$的长度。由$\pi(u,v,r)$的递归结构得出以下递推式:
我们的目标是计算所有顶点u和v的$dist(u,v,V)$。再一次,我们通过递推式得出动态规划运行时为$O(V^3)$。
正如我们之前的所有的最短路径动归算法,通过移除数组的第三个记忆维我们可以简化KleeneAPSP。也正是由于我们对顶点的数字标记是任意的,没有必要特意在伪代码中指出。我们修改后得到Floyd和Warshall的版本如下:
我们将FloydWarshall和我们之前稍慢的动态规划算法LeyzorekAPSP比较会发现有趣的事情。并非执行$O(logV)$次顶点三元组循环计算,FloydWarshall只执行一次就够了,但这仅仅是因为它的三个内层循环的嵌套顺序与后者不同。
结语
本文篇幅不算长,但分别从两种思维方式引导出常规的优化算法。其一使用单源算法来解决完全最短路径问题,不过Dijkstra的运行时明显优于Bellman-Ford却受制于负权边,这是一个优化点;其二就是我们熟悉的动态规划,由一般递推式得出的算法还是比较慢,因为我们通常的思路是把当前路径切割为一条路径和一条边,这又是一个优化点。但本文令我惊叹的时最后这个动归算法,思路就更巧妙了,完全不同于之前限制通过边的数量来令算法停止,而是限制通过确定的顶点,当然重点还是它挽救了我的颜面!😏
原文链接
http://jeffe.cs.illinois.edu/teaching/algorithms/book/09-apsp.pdf