前言
专门用一章来讲应用还真是少见,但这也说明流和割的应用确实是图算法的重中之重。我大概扫了一眼小标题,可以确定本篇涉及的内容应该与二分图的最大独立集和最小点覆盖问题类似。所以读懂本文应该不难,关键是了解什么样的应用场景会用到流和割。
知识点
边-不相交路径
最简单的最大流应用之一应该是使用最大流计算有向图G中从s到t的边-不相交路径的最大数量。在$G$中边-不相交路的集合径指的是每条$G$中的边只出现在最多出现在这个集合中的一条路径;多条边-不相交路径可能会通过同一顶点。
如果我们给与每条边的容量是1,那么从s到t的最大流通过每条边的流量不是0就是1。流分解定理表明由浸满边组成的子图$S$是一些边-不相交路径和环的集合。此外,流分解的路径数量和整个流的值是一样的。从S中移除真实路径是很简单的—沿着$S$中任意从s到t的有向路径移除它,并且递归执行此步骤。
相反,我们将任意k条边-不相交路径的集合转换成一个流,通过沿着每条从s到t的路径推入单元流;最后这个流的值是k。也就是说这种情况下计算最大流就是在计算边-不相交路径的最大数量。
如果我们使用Orlin算法来计算最大流,我们可以在$O(VE)$时间内计算出边-不相交路径,但是Orlin算法在此处实在是大材小用。因为割$(\{s\},V\backslash\{s\})$的容量最多是$V-1$,所以这里最大流的值最多是$V-1$。这样,Ford和Fulkerson的最原始的增广路算法的运行时正好是$O(|f^{*}|E)=\textbf{O(VE)}$。
同样的算法也可以用来解决无向图的边-不相交路径。首先,将每条$G$中无向边$uv$使用有向边$u\rightarrow v$和$v\rightarrow u$来代替,每条边都是单元容量,得到的这个图用$G’$表示。接下来,使用Ford-Fulkerson计算$G’$中的最大(s,t)-flow $f^{*}$。对于任意$G$中的边$uv$,如果$f^{*}$同时浸满了$G’$中的有向边$u\rightarrow v$和$v\rightarrow u$,我们可以从流中同时移除它们并且不改变流的值。(一般来说,通过去掉$G’$中的所有环我们可以找到一个有向无环的最大流,不局限于长度为2的环。)这样,为了不失普遍性,$f^{*}$在每条浸满边中的方向都是唯一的。最终,我们可以搜索由$f^{*}$的浸满有向边构成的子图找到边-不相交路径。
顶点容量和点-不相交路径
现在假设输入图G中顶点和边都有容量,根据我们的约束,对于每个除了s和t的顶点v,我们要求通过顶点v的流值最多是$c(v)$:
添加了顶点约束后我们还能计算出最大流吗?
在1962年,Ford和Fulkerson提出了一种可以将此情况约化出只有边容量的流网络$\overline{G}$。将每个顶点$v$使用两个顶点$v_{in}$和$v_{out}$及一条容量为$c(v)$的边$v_{in}\rightarrow v_{out}$,接着将有向边$u\rightarrow v$替换成边$u_{out}\rightarrow v_{in}$(保持原来的容量)。照例根据定义表明每一条$\overline{G}$中的可行的$(s_{out},t_{in})$-flow和原图$G$中可行的(s,t)-flow是相同的,并且反之亦然。特别是,每个$\overline{G}$中的最大流和$G$中的是一样的。将$G$约化成$\overline{G}$耗时为$O(E)$,然后我们在用Orlin算法计算$\overline{G}$的最大流。总体上,计算$G$的最大流耗时为$\textbf{O(VE)}$。
现在假设每个顶点的容量是1在计算最大流,得出从s到t的点-不相交路径的最大数量耗时为$O(VE)$!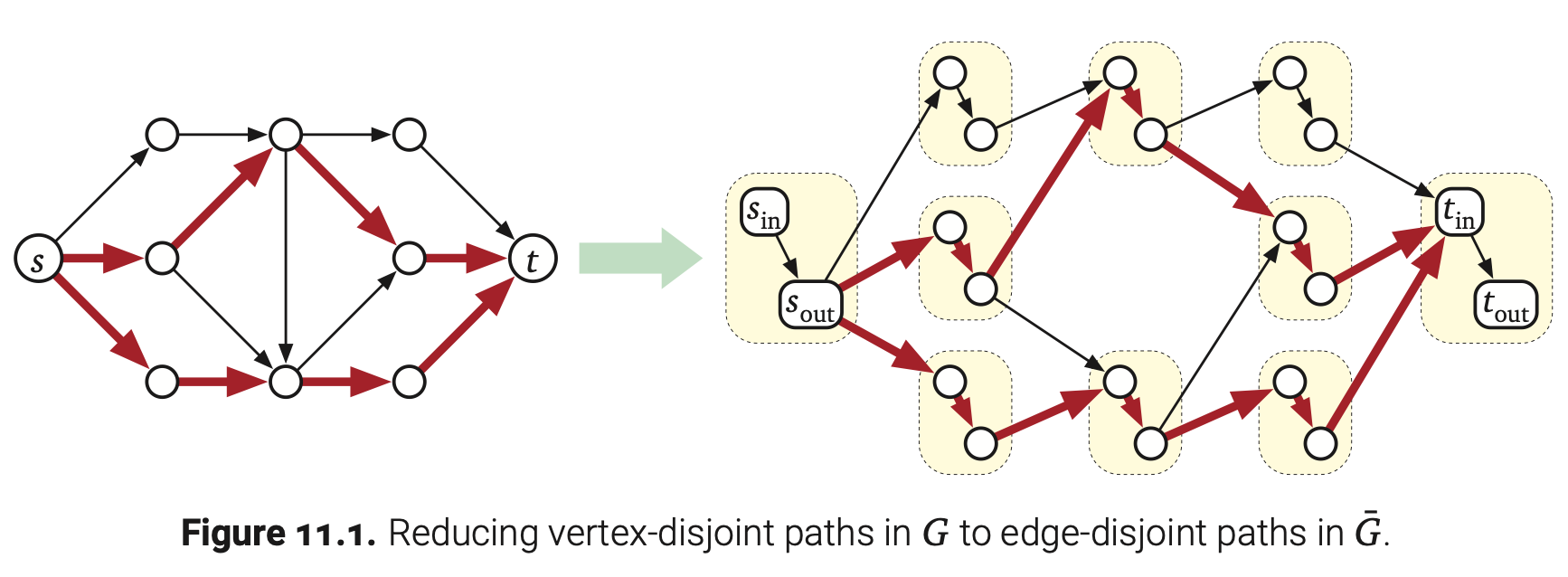
二分图匹配
另一个最大流的普遍应用是找到二分图中的最大匹配。一个匹配是一个子图,其中每个顶点的度不超过1,换个表达,一个边的集合,其中没有两条边共享一个顶点。此问题就是要找到边数量最多的匹配。
举例,假设有一些医生在寻找工作,正好也有一些医院在雇佣医生。每个医生列出他们想去工作的医院,每个医院也列出它们想雇佣的医生。我们的任务是找到一个最大的医生-医院的集合,并且医生和医院互相接受。这个问题就等同于在顶点为医生和医院的二分图中找到最大匹配,如果医院和医院彼此接受才能有关系边。
我们可以将这个问题约化成最大流问题。如下,用$G$表示集合$L\cup R$的二分图,每条边连接L和R中各一个顶点。通过(1)调整每条边的方向从$L$到$R$,(2)添加一个源点s以及到达$L$每个顶点的边,(3)添加一个汇点t以及来自$R$中每个顶点的边,我们构造了一个新的有向图$G’$。最后我们将$G’$中每条边的容量指定为1。
任意匹配$M$可以被转化成一个$G’$中的流$f_M$:对于每条$M$中的边$uw$,沿着路径$s\rightarrow u\rightarrow w\rightarrow t$推入一个单元流。这样的路径除了在s和t两处外都是是不相交的,所以得到的流是满足容量约束的。此外,这个流的值正好是M中匹配边的数量。
相反,考虑$G’$中的任意(s,t)-flow $f$,使用Ford-Fulkerson增广路径算法计算。因为边的容量是整数,Ford-Fulkerson算法为每条边分配一个整数流。此外,因为每条边都是单元容量,计算出来的流要么浸满($f(e)=1$)要么避开($f(e)=0$)$G’$中的每条边。最后,因为每一个单元流只能进入任意$L$的某个顶点然后从$R$中的某个顶点离开,这些从$L$到$R$的浸满边就是$G$中的匹配。匹配的大小正好是$|f|$。
这样,$G$中的最大匹配数量就等于$G’$中的最大流值,而且已知我们可以使用增广路径找到最大流,我们将最大匹配转化为最大流的耗时为$O(E)$。至于计算最大流的运行时则是$\textbf{O(VE)}$,Orlin或者Ford-Fulkerson任选一个。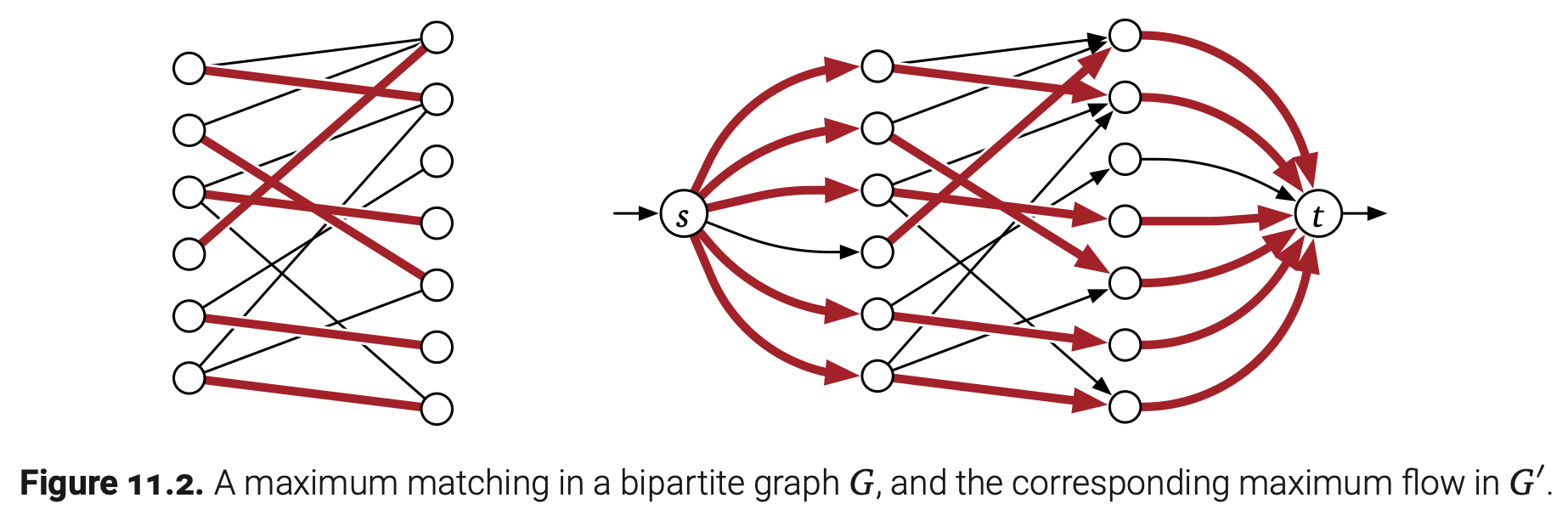
受到$G’$中Ford-Fulkerson算法的启发,我们得到了一种对应于原始二分图的算法。这个算法维护一个$G$中的匹配$M$,我们称一个G中的顶点已匹配仅当它是$M$中某条边的端点,否则就是未匹配。在这个算法的每次迭代中,我们在$G$中寻找一个交替路径—一个路径开始于$L$中的顶点,结束与$R$中的顶点,轮流通过不属于$M$的边和属于$M$的边。($G$中的交替路径正好对应着$G’$中当前流的增广路径)如果我们找到一条增广路径P,我们使用对称差$M\oplus P$来更新M,而且更新之后$M$增加了一条边,然后继续下一次迭代。如果当前没有增广路径了,根据最大流-最小割定理可知$M$就是最大匹配,所以算法该结束了。找到一条交替路径耗时为$O(E)$,并且算法不会超过$V$次迭代,所以总的算下来运行时为$\textbf{O(VE)}$。下图展示了算法的具体操作。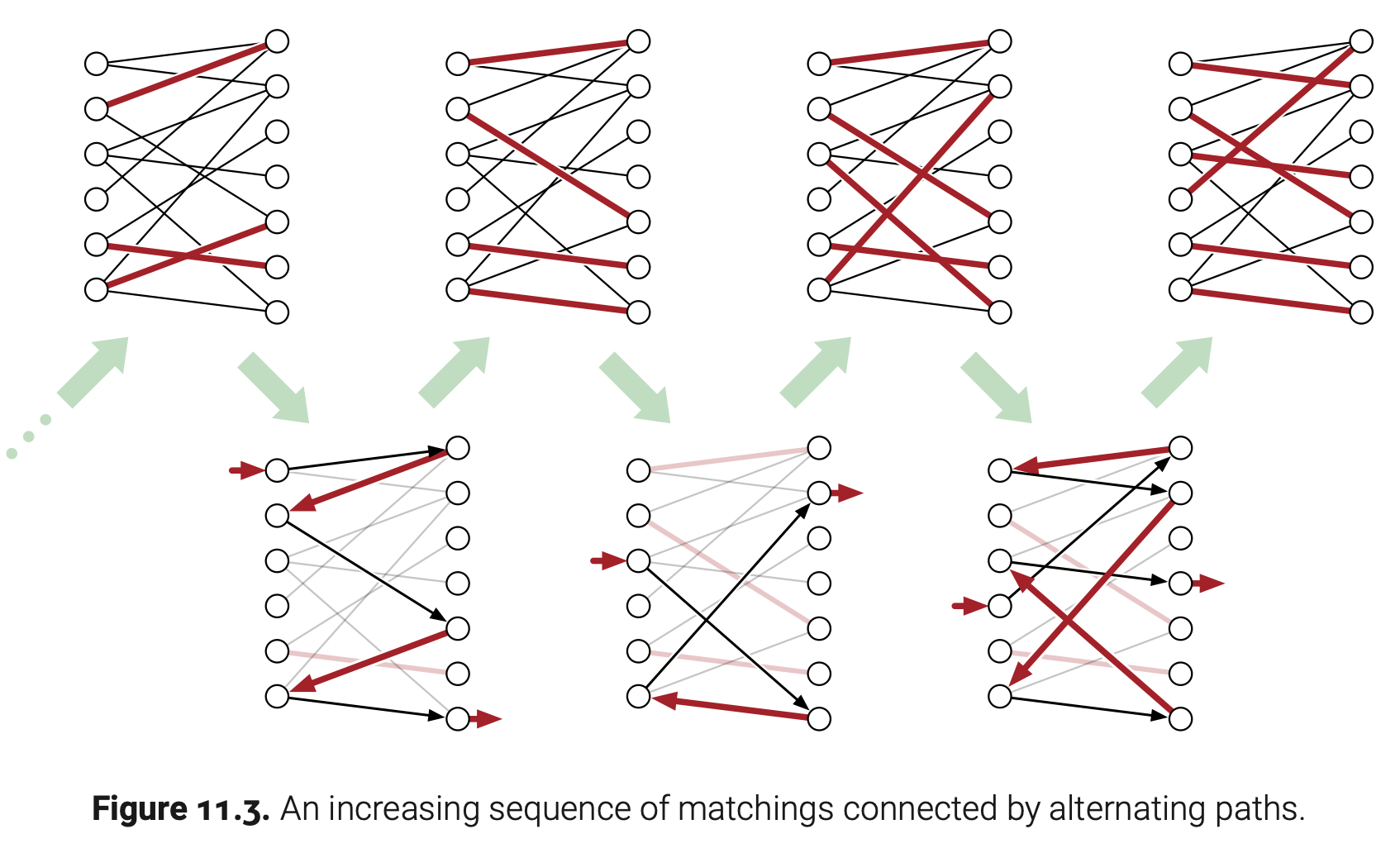
还有一个更为复杂的算法,由John Hopcroft和Richard Karp在1973年提出,计算二分图的最大匹配耗时仅需要$O(\sqrt{V}E)$,秘诀在于每次迭代找到多条不相交的交替路径。
元组选择
二分图最大匹配问题只是一种更为广泛类型的叫做元组选择问题的最简单的例子之一。元组选择问题的输入包括多个有限集合$X_1,X_2,…,X_d$,每个都代表一种不连续的资源。我们的任务就是找到最大数量的d-元组,每个都包含各个集合$X_i$的一个元素,受限于以下形式的容量约束:
- 对于每个索引i,每个元素$x\in X_i$只能出现在最多$c(x)$个已选元组中。
- 对于每个索引i,任意两个元素$x\in X_i$和$y\in X_{i+1}$只能出现在最多$c(x,y)$个已选元组中。
$c(x)$和$c(x,y)$中任意一个上界不是非负证书就是$\infty$。
在最大匹配问题中,我们有$d=2$个资源,每个元素$x$的容量是$c(x)=1$,每一对$(x,y)$的容量是$c(x,y)=1$或者$c(x,y)=0$,取决于边$xy$在所依赖的二分图中是否为存在。
因为资源是线性顺序的,只有相邻的两个集合$X_i$和$X_{i+1}$是相互约束的,元组选择问题可以可以被约化成有向图$G$中的最大流问题,定义如下: - $G$包含了每个集合$X_i$中的元素,以及源点s和汇点t。每个顶点(除了s和t)都有容量$c(x)$。
- 对于每个元素$w\in X_1$,$G$中都包含了边$s\rightarrow w$,对于每个元素$z\in X_d$也有边$z\rightarrow t$,以及对于有关i的每一对元素$x\in X_i$和$y\in X_{i+1}$都有容量为$c(x,y)$的边$x\rightarrow y$。(有必要的话可以删除容量为$c(x,y)=0$的边$x\rightarrow y$)
在$G$中每条从s到t的路径对应一个我们可以选择的d-元组;相反每个满足状态约束的可选d-元组也对应着$G$中一条从s到t的路径。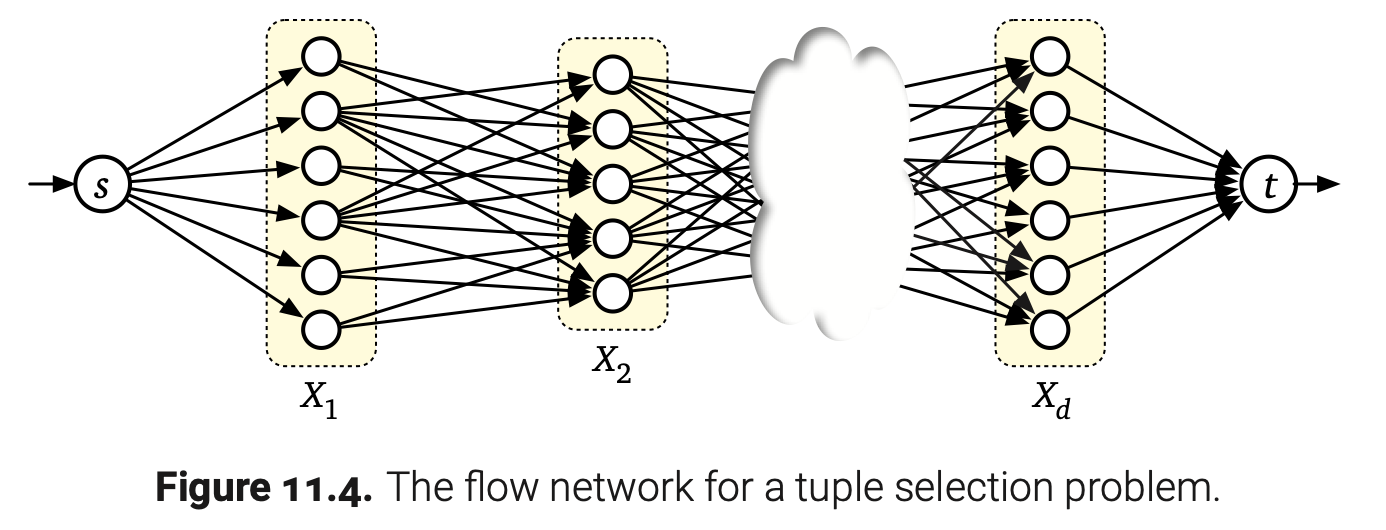
一般来说,用$f$表示G中的任意可行的整数(s,t)-flow。因为所有的容量都是整数或者$\infty$,根据流分解定理可知$f$是$|f|$条从s到t的路径总和,每条都带有一个单元的流量。根据定义又得出得到的元组都满足所有的容量约束。相反,对于任意k个满足容量约束的元组,k条相应路径的总和有事一个值为k的可行整数(s,t)-flow。
这样,我们可以通过计算$G$中最大的(s,t)-flow $f^{*}$来选择满足容量约束的最大数量元组,然后计算$f^{*}$的流分解。因为$G$中所有有限容量都是整数,为了不是普遍性,我们可以假设$f^{*}$是一个整数流,因此(根据上个段落)它对应的是$|f^{*}|$个有效元组。
考试排程
接下来的“真实世界”排程问题也许可以帮我们阐明我们的普遍约化。
Sham-Poobanana大学雇佣了你写一个算法来安排他们的期末考试。有n个不同的班级,每个都需要在某个时间点从r个教室中选择一个作为考场;相反,每个班级不能分成多个教室或者多个时间点考试。此外,每个考试需要一位老师监考。每个老师同一时间只能监考一场考试;每个老师都有确定的时间空挡可以监考;而且每个老师监考不能超过5场。这个排程为题的输入包含三个数组:
- 一个整数数组$E[1..n]$,$E[i]$表示第i个班级的学生数量。
- 一个整数数组$S[1..r]$,$S[j]$表示第j个教室的座位数量。第i个班级可以在第j个教室考试当且仅当$E[i]\leq S[j]$。
- 一个布尔数组$A[1..t,1..p]$,$A[k,l]=true$当且仅当第l个老师第k个时间空挡是空闲的。
用$N=n+r+tp$表示输入的空间大小,你的工作就是设计一个算法为每个班级安排一个时间点、一个教室、一个监考老师。或者正确报告此条件下不能排程。
这是一个基于四种资源的标准元组选择问题:班级、教室、时间点、老师。为了解决这个问题,我们构造一个带有六种类型顶点的流网络$G$ — 一种为源点$s’$,一种为班级顶点$c_i$,一种为教室顶点$r_j$,一种是时间顶点$t_k$,一种是老师顶点$p_l$,一种为汇点$t’$ — 以五种类型的边,如下图所示: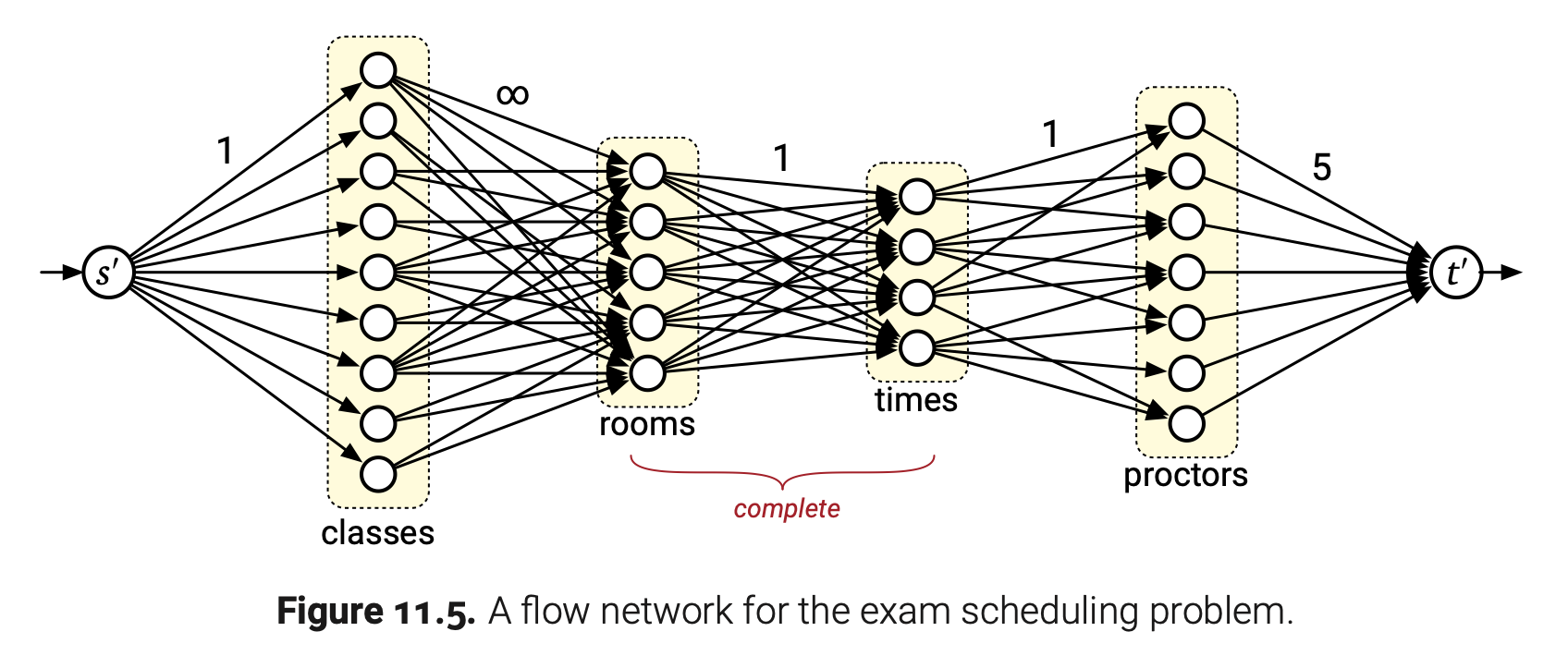
- 边$s’\rightarrow c_i$的容量是1,i表示班级的序号。(每个班级最多一个期末考试)
- 边$c_i\rightarrow r_j$的容量是$\infty$,j是教室的序号,并且$E[i]\leq S[j]$。(第i个班级可以在第j个教室考试当且仅当教室有充足的座位)此处是仅有的$E[i]$和$S[j]$使用的位置。
- 边$r_j\rightarrow t_k$的容量是1,k是时间段序号。(在时间段k教室j中只能有一场考试)
- 边$t_k\rightarrow p_l$的容量是1,l是老师序号,并且$A[l,k]=true$。(一个老师只能在同一时间监考一场考试,并且还要有空才行)
- 边$p_l\rightarrow t’$的容量是5。(每个老师只能监考5次)
(此处使用$s’$和$t’$作为源点和汇点是因为问题描述中我们已经使用t来表示时间点了)总的来说,$G$有$n+r+t+p+2=O(N)$个顶点和$O(nr+rt+tp)=O(N^2)$条边。
$G$中每条从$s’$到$t’$的路径代表一场考试唯一的班级、教室、时间和老师的有效选择;特别是,教室可以容下班级,老师在指定时间有空。相反,对于每个有效选择(班级、教室、时间、老师),都有一条$G$中对应的从$s’$到$t’$的路径。这样,通过计算$G$中的最大流$(s’,t’)$-flow $f^{*}$,我们构造了一个最大数量考试的有效排程,将$f^{*}$分解为从$s’$到$t’$的路径,然后从每个路径中抄写出班级-教室-时间-老师的分配。如果$|f^{*}|=n$,我们可以返回排程结果;否则我们可以正确报告无法为n场期末考试排程。
根据输入数据构造$G$耗时为$O(E)$。我们可以使用Ford-Fulkerson(因为$|f^{*}|\leq n< V$)或者Orlin算法在$O(VE)$时间内计算出最大流。如此,我们的算法总运行时为$O(VE)=\textbf{O(N^3)}$。
不相交路径覆盖
有向图$G$的路径覆盖是一些$G$中有向路径的集合,每个$G$中的每个顶点至少出现在一条路径中。有向图$G$的不相交路径覆盖是一种路径覆盖,要求每个$G$中的顶点只出现在某一条路径中。每个有向图都都包含一种简单的路径覆盖,由多个长度为零的路径组成,但是没有什么探讨价值。相反,我们更希望找到数量最少的路径覆盖。一般来说这是一个NP-困难问题 — 一个图的不相交路径覆盖数量为1当且仅当它包含了一条汉密尔顿路径 — 但是对于有向无环图还是存在一种基于流的高效算法。
为了解决有向无环图$G=(V,E)$中的这个问题,我们构造一个新的二分图$G’=(V’,E’)$如下。
- 对于每个$G$中的顶点v, $G’$包含两个顶点$v^{\flat}$和$v^{\sharp}$。
- 对于每条$G$中的有向边$u\rightarrow v$,$G’$包含一条有向边$u^{\flat}v^{\sharp}$。
(如果$G$是使用邻接矩阵表示的,那么$G’$正好也可以用同样的邻接矩阵来表示。)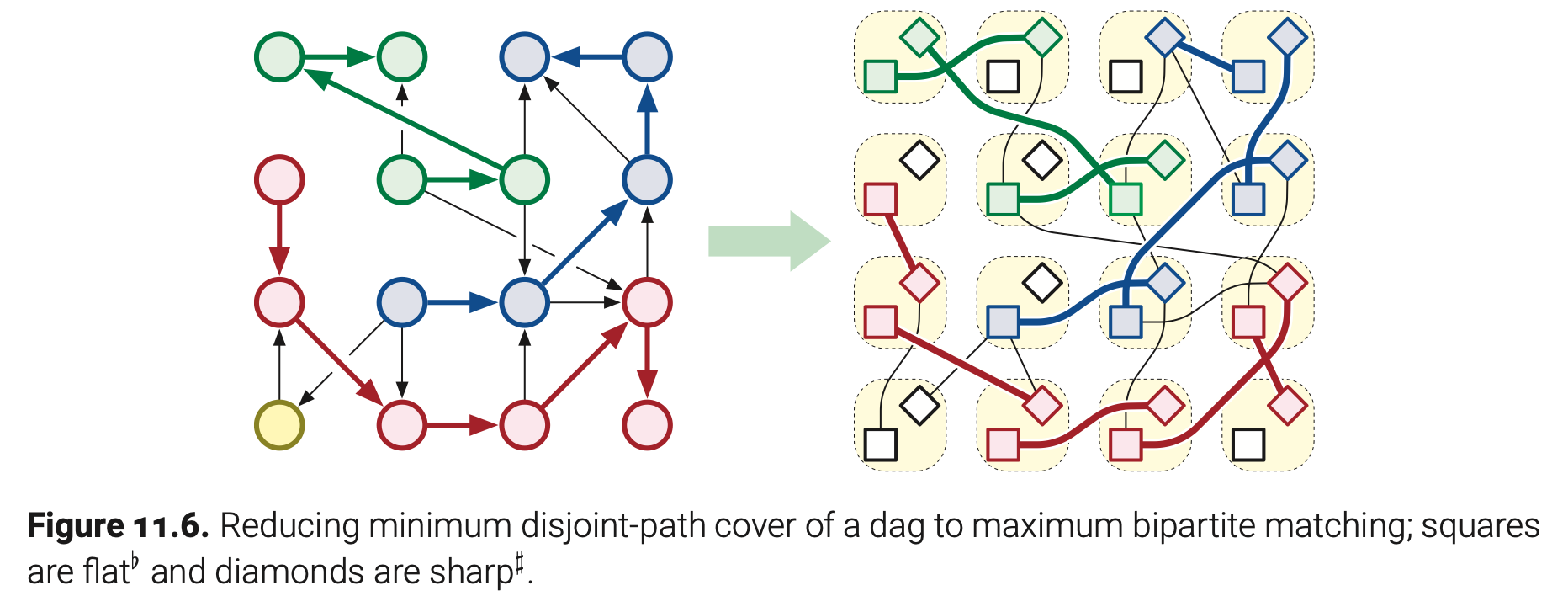
现在我宣布$G$可以被k条不相交路径覆盖当且仅当$G’$中存在大小为$V-k$的匹配。通常,我们分两个阶段来证明这个等价关系:
$\Leftarrow$ 假设$G$有一个包含k条路径的路径覆盖$P$;将$P$视为$G$的一个子图。每个$P$中的顶点入度不是0就是1;此外,$P$中的每条路径恰好有一个顶点的入度是0。也就是说$P$包含了正好$V-k$条边。现在顶一个一个包含$G’$中边的集合$M$如下:
根据不相交路径覆盖的定义,每个$G$中的顶点最多有一条在$P$中的进入边和一条在$P$中的离开边。我们推断每个$G’$中的顶点最多与一条$M$中的边相关;也就是$M$数量是$V-k$。
$\Rightarrow$ 假设$G’$有一个大小为$V-k$的匹配$M$。对应地定义一个$G$的子图$P=(V,M’)$,$M’$如下所示:
根据匹配的定义,每个$G$中的顶点在$P$中最多有一条进入边和一条离开边。也就是说$P$是$G$中不相交路径的集合;因为$P$包含了所有顶点,$P$定义了一个有$V-k$条边的不相交路径覆盖。$P$中路径的数量正好是$G$中没有$M’$中的边进入的顶点数量。我们推断$P$正好包含了k条路径。
接下来我们通过计算$G’$中的最大匹配就能找到$G$中的最小不相交路径覆盖,使用Ford-Fulkerson的最大流算法在$O(V’E’)=\textbf{O(VE)}$时间内就能找到。
尽管描述的是以有向无环图和路径为措辞,但这确实是一个最大匹配问题:我们想在图中找到尽可能多的有明确后继的顶点。覆盖有向无环图的路径数量等于没有后继的顶点数量。(当然每个二分图最大匹配问题就是一个流问题)
最少教员雇佣
让我们回到Sham-Poobanana大学的另一个“真实世界”排程问题。学校每天提供了大量的课程。因为财政原因,学校需要降低教员数量。然而学生们已经交了学费(学校没钱请律师打官司),学校需要保留充足的教师数量来保证已公布课程的正常执教。学校应该保留多少教师呢?每个留校的教师会在任意时间被安排一系列课程。被分配到每个教授的课程不能重叠;此外,必须在教师的课程之间留有充足的时间,让他们能从一个教室走到下一个。为了这个问题,让我们假设每个教师精通所有课程,并且他们没有办公室,午餐或者上厕所的时间。
具体地假设有n个课程以及m个不同的地点。此问题输入的数据结构如下:
- 一个课程数组$C[1..n]$,$C[i]$有三个字段:$C[i].start$是开始时间,$C[i].end$是结束时间,$C[i].loc$是上课地点。
- 一个二维数组$T[1..m,1..m]$,$T[u,v]$表示从地点u到地点v的耗时。
我们想要找到可以正常执教课程的教师最低数量,那么一个教师被安排了两个课程i和j,$C[j].start\geq C[i].start$,我们还要保证
我们可以将此问题约化为不相交路径覆盖问题来解决。我们构造一个有向无环图$G=(V,E)$,课程作为定点,边代表两个课程是否能够由同一位教师来上。特别是,有向边$i\rightarrow j$表示同一教师可以先教课程i再教课程j。可以再$O(n^2)$时间内暴力构造这个有向无环图。然后使用上述的匹配算法找到一个不相交路径覆盖;每个$G$中的有向路径代表着一个教师的课程计划。整个算法的运行时为$(n^2+VE)=\textbf{O(n^3)}$。
尽管开始的描述是以时间和距离为措辞,但这的确是一个最大匹配问题(也就是最大流问题)。特别是我们想为同一个教师安排尽量多的课程。我们需要的教师数量等于没有分配后继的课程数量;每个没有后继的课程就是同一教师上的最后一课。
棒球淘汰赛
每年数以百万的棒球迷都在热心的关注自己喜欢的球队,希望他们可以在季后赛中出线,最后参加世界级赛事。不过大多数队伍都会被“理论淘汰”,一般是在此之后的几天或者常规赛季结束之前。通常,很容易看出一个队伍被淘汰时候 — 在他们的角度来看无法赢得足够的分数追赶上领先的队伍。但有时候情况会非常微妙。比如,下面是1996年的八月美国东部棒球联赛的战绩。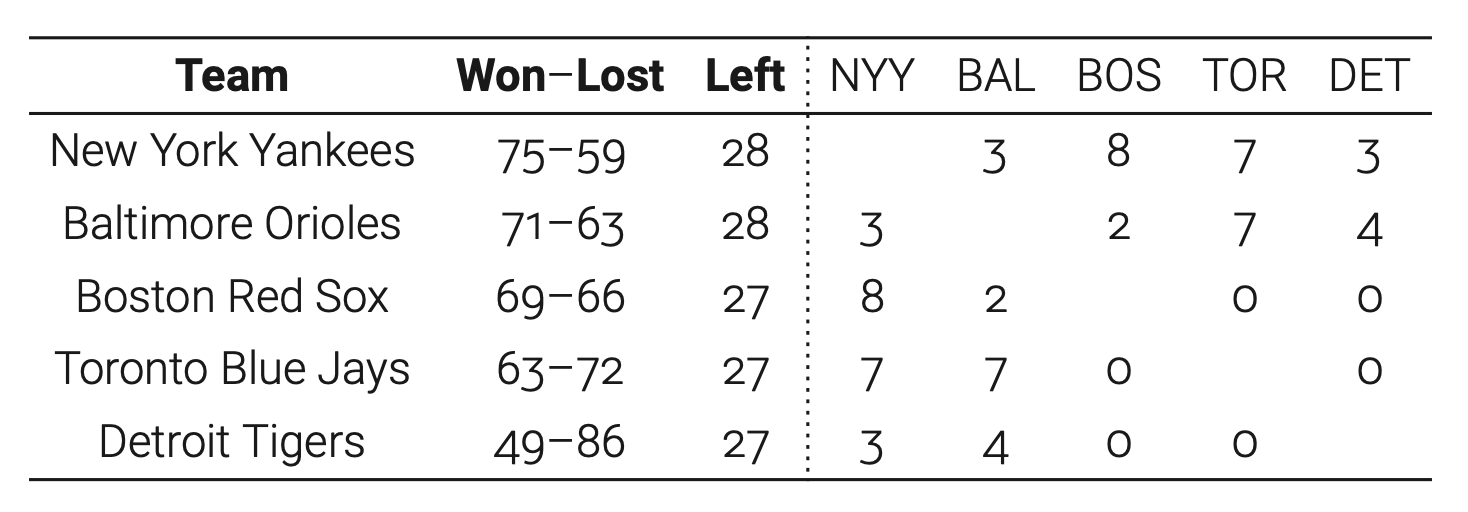
Detroit明显是落后的,但是仍然有一些铁粉希望他们能获胜。毕竟,如果Detroit赢了剩下的27场比赛,他们的赛季将以76胜结束,超过其他队伍目前的胜场。所以只要别的队伍输掉接下来的每场比赛 … 但这是不可能的,因为剩下的比赛是要互相进行的。下面有一个完成的讨论:
通过赢得所有剩下的比赛,Detroit就会以76-86的战绩结束本赛季。如果NewYork只赢得剩下场次中的两场,他们就会以77-85的战绩结束,并且还超过了Detroit。所以我们假设Detroit剩余场次不败并且NewYork不胜。
在这个剧本下NewYork和Boston之间还有八场比赛。如果Boston赢得这些比赛,他们至少会以77胜结束赛季,领先于Detroit。这样,Detroit任然有得第一机会的方式是NewYork在与Boston的比赛中只胜一场,其余的都输掉。同时Boston还要输掉与Yankees之外的比赛。这就创造一种三队同分领先的情况。
现在看看在我们的剧本中Baltimore和Toronto之间会发生什么。Baltimore和Boston有两场比赛,和NewYork有三场。所以如果按以上描述发展,Baltimore至少会以76胜收尾。所以Detroit能追上Baltimore仅当Baltimore输掉其余的比赛。这就是说Baltimore必须输掉与Toronto的七场比赛。前面我们已经提到Toronto也要赢下与NewYork之间的七场比赛。但是如果是这样,Toronto就会以77-85的成绩收尾,领先于Detroit。所以,不管发生什么,Detroit都无法从美国东部棒球联赛中获得第一。
我们有更好的方式来解决这个问题。
关于这个问题有一个更为抽象的描述。我们的输入有两个数组$W[1..n]$和$G[1..n,1..n]$组成,$W[i]$表示第i个队伍目前的胜场,$G[i,j]$表示队伍i和j之间剩余场次。我们想要判断第n个队伍是否能本赛季获得第一。
在1960年代中期,Benjamin Schwartz观察到这个问题可以改造为一个最大流问题;大约20年后又有一些人把Schwartz的想法简化成了一个成对选择问题。特别是,我们想要知道有没有可能为每场比赛选一个胜者,然后第n队就变成了第一。用$R[i]=\sum_j G[i,j]$表示第i对的剩余场次。那么第n队获得第一当且仅当每个队伍i赢得不超过$W[n]+R[n]-W[i]$场比赛。
因为我们想要为每场比赛选择一个获胜队伍,我们先构造一个二分图,顶点代分别是队伍和比赛。我们有$\dbinom{n}{2}$个比赛顶点$g_{i,j}$,并且$1\leq i< j< n$,还有$n-1$个队伍顶点$t_i$,并且$1\leq i< n$。对于每一对i和j,我们添加容量无限的边$g_{i,j}\rightarrow t_i$和$g_{i,j}\rightarrow t_j$。我们添加一个源点s,再为每场比赛添加容量为$G[i,j]$的边$s\rightarrow g_{i,j}$。最后我们添加一个汇点t,再为每个队伍添加容量为$W[n]+R[n]-W[i]$的边$t_i\rightarrow t$。
下图就是关于1996年美国东部棒球联赛的战绩图,第n队就是Detroit。所有未标注的边都是无限容量。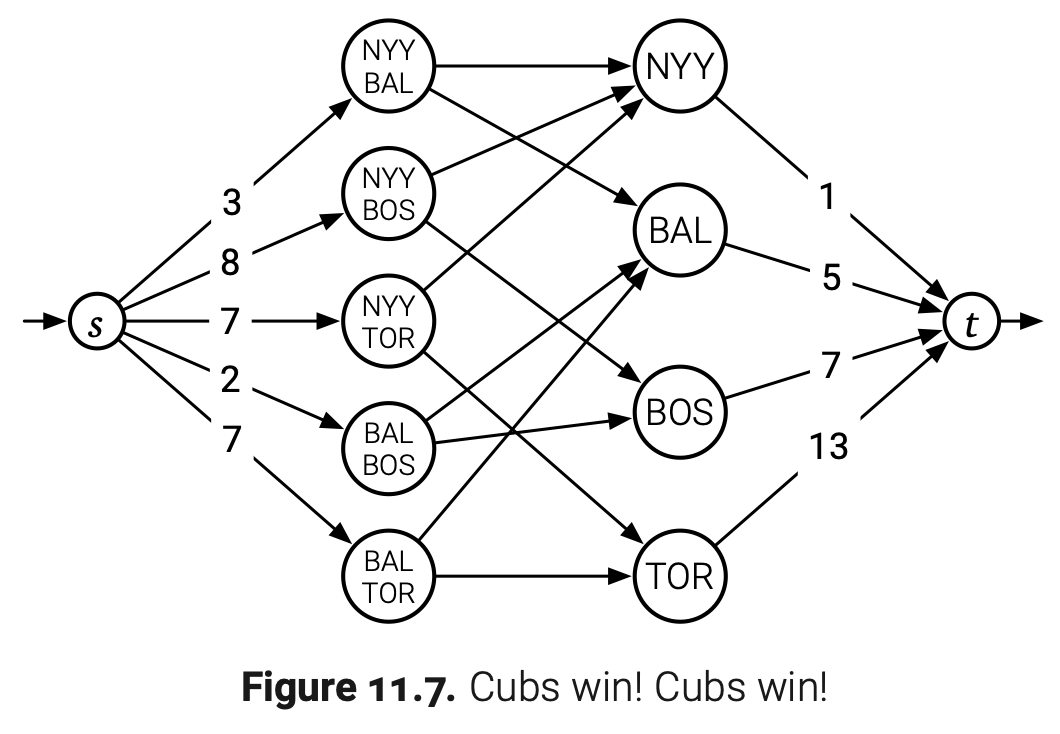
定理. 第n队可以在赛季结束获得第一当且仅当上图中存在一个可行流并且它浸满了每条离开s的边。
证明: 假设对于第n队有可能在赛季结束获得第一。那么每个$i<n$的队伍最多赢得$W[n]+R[n]-W[i]$场比赛。对于队伍i和j之间的胜者,沿着路径$s\rightarrow g_{i,j}\rightarrow t_i\rightarrow t$添加一个单元流。因为队伍i和j之间正好有$G[i,j]$场比赛,每条离开s的边都会被浸满。因为每个队伍i只能赢$W[n]+R[n]-W[i]$场比赛,所以得到的流是可行的。
相反,用$f$表示浸满所有s的离开边的流。假设对于所有i和j,队伍i赢得了恰好$f(g_{i,j}\rightarrow t_i)$场对抗队伍j的比赛。那么队伍i和j对抗了$f(g_{i,j}\rightarrow t_i)+f(g_{i,j}\rightarrow t_j)=f(s\rightarrow g_{i,j})=G[i,j]$场比赛,所以每场以后的比赛都打了。此外,每个队伍i赢得了$\sum_j f(g_{i,j}\rightarrow t_i)=f(t_i\rightarrow t)\leq W[n]+R[n]-W[i]$场以后的比赛,因此胜场不超过$W[n]+R[n]$。如此,如果队伍n赢得所有以后的比赛,他们就可以获得赛季第一。
总之,为了判断我们喜欢的队伍是否能赢,我们构造流网络,计算最大流,看看最大流是否浸满了所有s的离开边。比如,棒球联赛的图中,s的离开边总容量是27。另外,t的进入边的总容量是26,也就是说最大流的值不超过26。我们推断Detroit就被“理论淘汰”了。
流网络的顶点数为$O(n^2)$,边数为$O(n^2)$,构造时间为$O(n^2)$。使用Orlin算法,我们可以在$O(VE)=\textbf{O(n^4)}$时间内计算出最大流。
这并不是棒球淘汰问题的最快算法。在2001年,Kevin Wayne证明可以在$\textbf{O(n^3)}$时间推断所有队伍是否在理论上被淘汰,基于单次最大流计算。
项目挑选
这是最后一个案例了,假设提供n个项目给我们挑选。一些项目必须等某些项目实施完成才能开工。项目的依赖关系可以被描述为一个有向无环图$G$,顶点是项目,边$u\rightarrow v$表示项目u不能在v之间实施。最后,每个项目v完成之后都有一定的收益$¥(v)$;一些项目是负数收益,我们可以理解为正数付费。我们可以选择完成所有项目的任意子集$X$,当然每个项目x所依赖的项目也在$X$中。我们的目标是找到一个收益最大的有效子集。特别注意,如果所有项目都是负数收益,正确答案应该是什么也不做。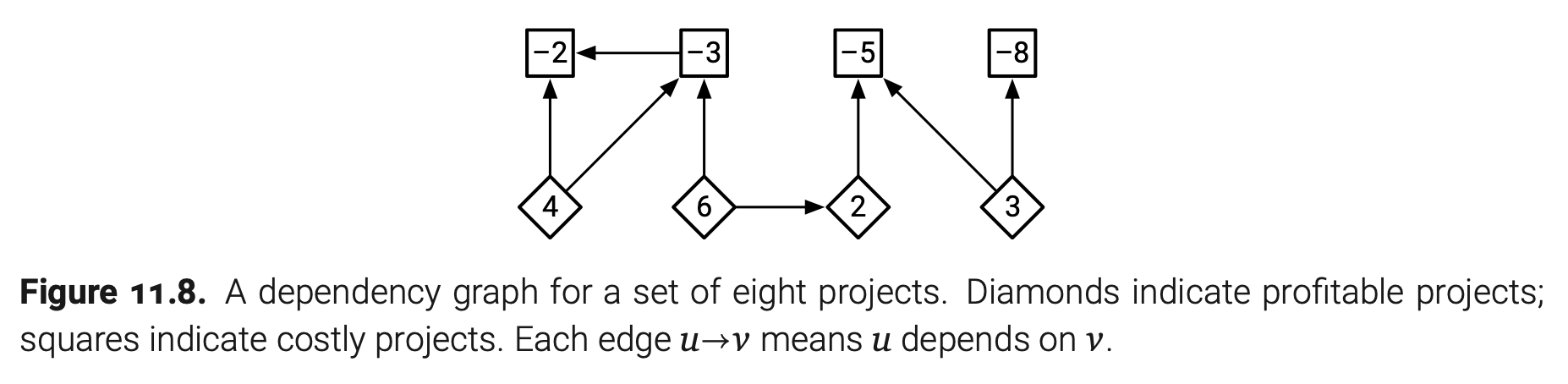
在较高水平下,我们的任务是将所有任务划分为两个子集$S$和$T$,分别代表我们选择和抛弃的项目。所以直观上,我们更想要把此问题约化成确定图中的最小割问题。但是怎样构图?如何执行先决条件?我们想要最大化收益,但我们只知道怎样找到最小割。还有负数收益怎么转变成正数容量?
为了将我们的约束图$G$转变成流网络$G’$,我们需要添加源点s和汇点t到依赖图中,为每个正数收益的项目($¥(v)>0$)添加边$s\rightarrow v$,为每个负数收益($¥(u)<0$)的项目添加边$u\rightarrow t$。直观上,我们认为将s认为是一个新的项目,收益和付费都为0,而且必须实施。我们如下分配$G’$中边的容量:
- 对于每个收益项目,有$c(s\rightarrow v)=¥(v)$;
- 对于每个付费项目,有$c(u\rightarrow t)=-¥(u)$;
- 对于每个依赖边,有$c(u\rightarrow v)=\infty$;
所有边的容量都是整数,所以这是一个最小割问题的有效输入。
现在考虑$G’$中的任意(s,t)-cut $(S,T)$。对于原依赖图中的任意边$u\rightarrow v$,如果$u\in S$并且$v\in T$,那么$||S,T||=\infty$。这样,我们就可以合理地选择$S$中的项目当且仅当$(S,T)$的容量是有限的。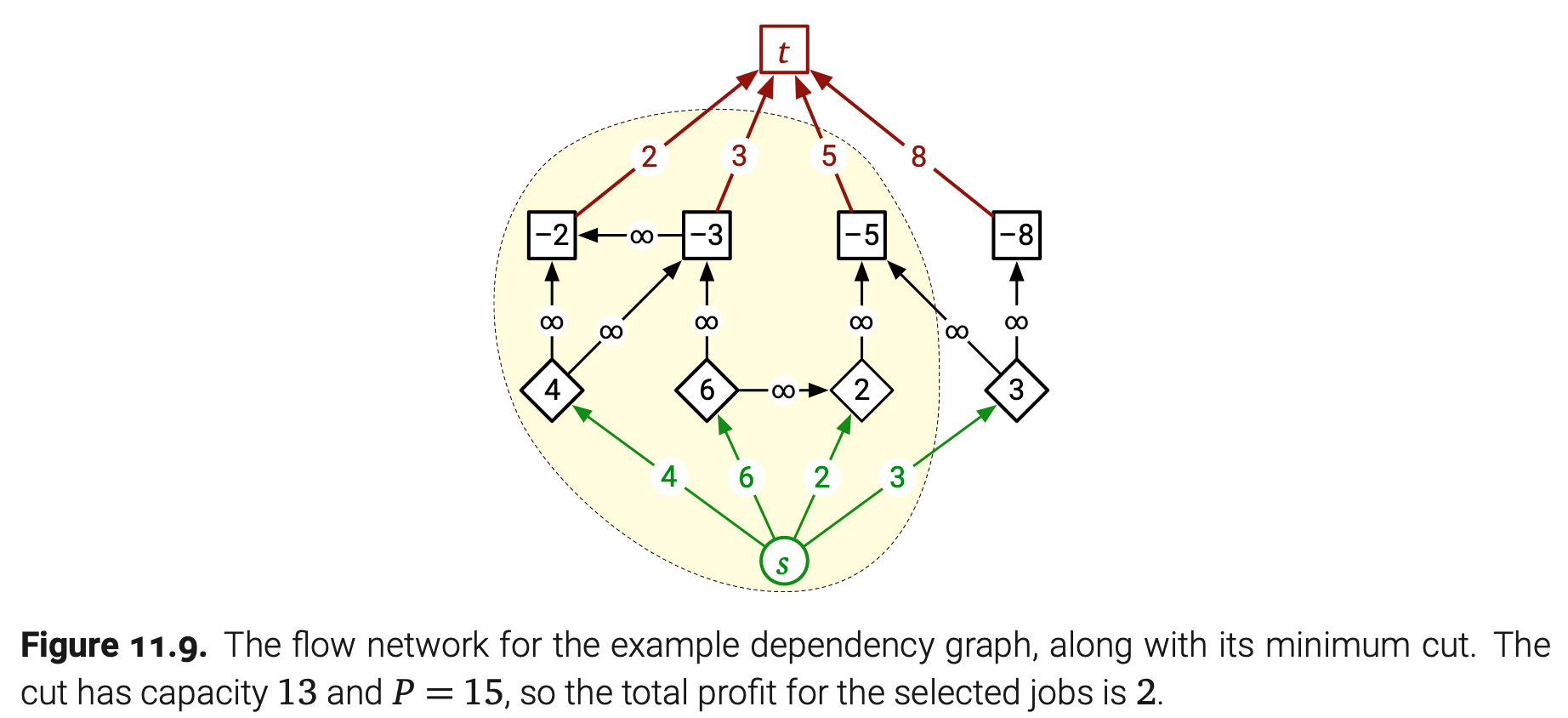
事实上,容量越小的割对应的项目收益也越高。尤其是,我宣布$S$中的项目总收益是$P-||S,T||$,$P$是所有整数收益项目的和:
我们可以根据定义直接证明。对于任意子集$X$,我们定义三个值。(通常,如果$c(u\rightarrow v)=0$,我们认为$u\rightarrow v$这条边不存在)
根据定义,$P=yield(V)=yield(S)+yield(T)$。因为$(S,T)$的容量是有限的,只有$s\rightarrow v$和$u\rightarrow t$这样的边被切割。根据前面的构造,每条边$s\rightarrow v$指向的是一个正数收益项目,$u\rightarrow t$指向负数收益项目。这样$||S,T||=cost(S)+yield(T)$。我们马上可以得到$P-||S,T||=yield(S)-cost(S)=profit(S)$。
也就是说通过计算$G’$中的最小割可以最大化我们的总收益。我们可以在$O(V+E)$时间内轻松构造$G’$,使用Orlin算法计算最小割的时间是$O(VE)$。我们得到整个项目挑选算法的运行时为$\textbf{O(VE)}$。
结语
本章并没有什么新知识点可以学习,或者说有,但并不是三言两语能说清的。通篇看下来都是在作经验之谈,也没有什么约定俗成的解决套路。重点就在于如何使用约化。关于这个东西就真的是仁者见仁智者见智了,个人的理解不同,解决问题的方向也就不同。约化的方式没有最好,只有更好!
原文链接
http://jeffe.cs.illinois.edu/teaching/algorithms/book/11-maxflowapps.pdf