前言
这节课的重点在于非确定性优先自动机(NFA)模型以及它与DFA模型的关系。
非确定性是计算理论中极为重要的概念。他指的是在一个计算中,不同的阶段可能会有多种选择的可能性。那么我们会思考这些选择的可能得到的输出,通常集中在是否存在一系列选择,它会导向一个特别的输出(比如一个有限自动机的接受状态)。
这听起来像是一种幻想的设计,不太可能与实际观点相关,因为现实的计算机不会做非确定性选择:在每一步中显示计算机做出的选择由已给定的配置决定。然而相反我们对非确定性最大的兴趣不在于给出建议。我们将会发现非确定性是一个强大的分析工具(从某种意义上,他帮助我们设计事物和证明事实),它与证明和验证的密切联系具有基本的重要性。
知识点
非确定性有限自动机基础
关于NFA模型的讨论,我们从定义开始。这个定义和DFA模型类似,但有一个关键的不同点。
定义3.1. 一个非确定性有限自动机(或者简称NFA)是一个5-元组
$Q$是一个有限非空的状态集合,$\Sigma$是一个字母表,$\delta$是一个转移函数,它的形式为
$q_0\in Q$是一个初始状态,$F\subseteq Q$是一个接受状态集合。
两个定义之间的关键不同点和与DFA的类似定义是转移函数的形式不同。对于DFA的$\delta(q,a)$是一个状态,对于任意的选择,$q\in Q$和$a\in\Sigma$,代表着如果DFA处于状态$q$然后读取符号$a$将要转移的下一个状态。对于一个NFA,每个$\delta(q,a)$不是一个状态,而是一个状态的子集,就相当于$\delta(q,a)$是幂集$\mathcal{P}(Q)$中的一个元素。这个子集代表着所有NFA从状态$q$读取符号$a$后能转移的可能状态。这个子集中可能只有一个状态,或者有很多状态,或者根本没有状态 — 可能存在$\delta(q,a)=\varnothing$。
NFA不止为每一对$(q,a)\in Q\times\Sigma$定义了转移函数,也能同样为$(q,\varepsilon)$定义了转移函数。这里,本课程中总是如此,$\varepsilon$表示空字符串。根据定义$\delta$每个状态都有$\varepsilon$-转移,NFA不需要从输入中读取符号就可以从一个状态转移到另一个。
状态图
与DFA类似,我们有时候会用状态图来表示NFA。这次,对于每个状态$q$和每个符号$a$,会有多个标有$a$箭头从状态$q$的圆圈导出,这就告诉了我们$\delta(q,a)$中包含了那些状态,或者当$\delta(q,a)=\varnothing$就没有箭头。我们也会将箭头标上$\varnothing$,他表示$\varepsilon$-转移。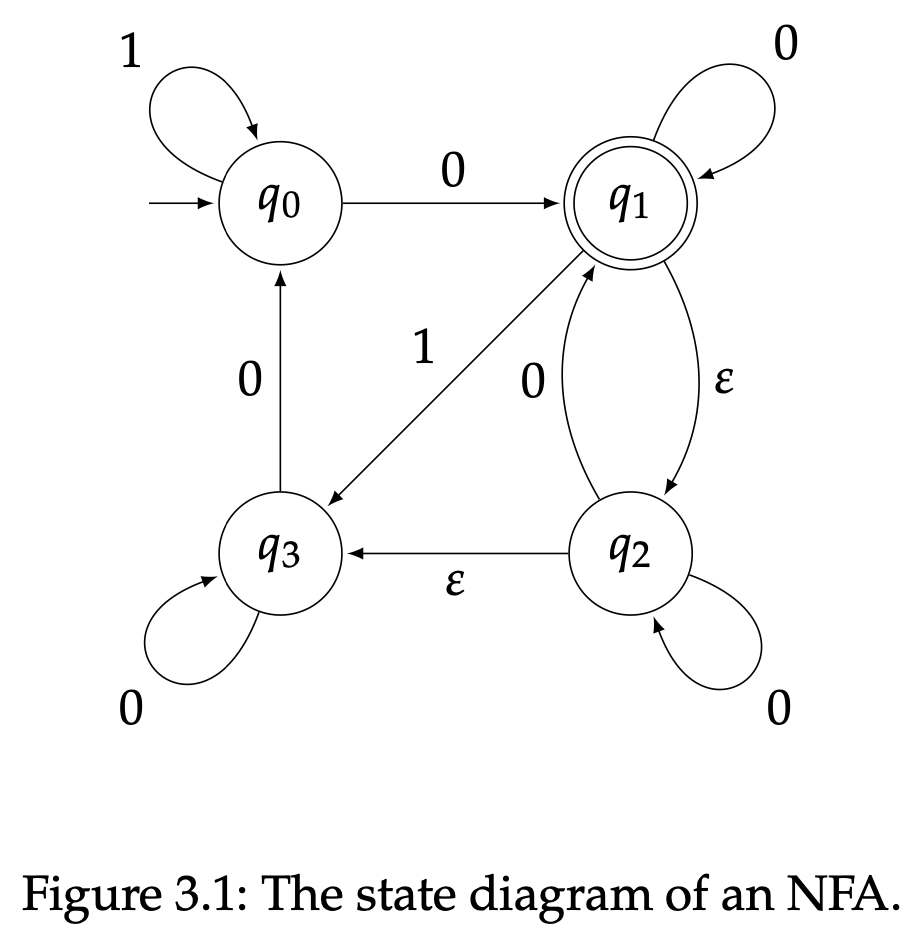
图3.1给出了一个NFA的状态图例子,在这个图中,我们发现$Q=\{q_0,q_1,q_2,q_3\}$,$q_0$是初始状态,$F=\{q_1\}$,如果这个图表示DFA,我们也是得到这些。我们有理由猜想这个图中的NFA的字母表是$\Sigma=\{0,1\}$,尽管能确定的是$\Sigma$中包含了符号0和1;比如也可能$\Sigma=\{0,1,2\}$,但对于每个$q\in Q$就应该出现$\delta(q,2)=\varnothing$。然而,让我们达成一致,除非我们另外明确声明,状态图中NFA只包含了图中所标的这些符号(当然$\varepsilon$除外),所以对于这个例子$\Sigma=\{0,1\}$。转移函数的形式为
得自于
NFA计算
接下来我们讨论一下NFA的接受和拒绝的定义。这次我们直接从正式定义开始,然后在尝试去理解它。
定义3.2. $N=(Q,\Sigma,\delta,q_0,F)$是一个NFA,$w\in\Sigma^{*}$是一个字符串。NFA $N$接受$w$当且仅当存在一个自然数$m\in\mathbb{N}$,一个状态序列$r_0,…,r_m$,和一个符号或者空字符串的序列$a_1,…,a_m\in\Sigma\cup\{\varepsilon\}$使得下面语句都成立:
- $r_0=q_0$.
- $r_m\in F$.
- $w=a_1\cdot\cdot\cdot a_m$.
- 对于每个$k\in\{0,…,m-1\}$有$r_{k+1}\in\delta(r_k,a_{k+1})$.
如果$N$不接受$w$,那么我们$N$拒绝了$w$。
正如你所知,我们可以将NFA对于字符串$w$的计算想成是一个单人游戏,目标是从初始状态出发,一步一步地转移状态,最后停在接受状态上。如果你想从状态$q$移动到状态$p$,可以通过两种方式:你可以从输入中读取一个符号$a$,已知$p\in\delta(q,a)$;或者你可以不读取符号,已知$p\in\delta(q,\varepsilon)$(存在一个从$q$到$p$的$\varepsilon$-转移)。为了赢得游戏,你不仅要停在接受状态上,而且还要读取完所有输入字符串$w$的符号。也就是说$N$接受$w$表示相应的游戏是可以获胜的。
定义3.2本质上就是我们讨论的游戏取胜的正式概念:自然数$m$代表着你移动的步数,$r_0,…,r_m$代表着访问过的状态。为了赢得游戏,你必须从状态$q_0$出发,并且停在一个接受状态上,这是为什么定义要求$r_0=q_0$和$r_m\in F$,在游戏结束前输入中的每个符号都已被读取,这也是为什么定义要求$w=a_1,…,a_m$。条件对于每个$k\in\{0,…,m-1\}$有$r_{k+1}\in\delta(r_k,a_{k+1})$对应的每一步都是有效转移。
我们需要花时间来说明当$m=0$时这个定义是如何起作用的。自然是包含0,所以没什么能阻止我们考虑$m=0$时,字符串也能被接受。如果我们从$m=0$开始,我们必须考虑状态序列$r_0,…,r_0$和符号或者空字符串序列$a_1,…,a_0\in\Sigma\cup,\{\varnothing\}$的存在,不管这些序列是否满足上面定义中列出的四个要求。状态序列的形式$r_0,…,r_0$并没有什么错误,我们只是为了表现这个序列只有一个元素。另外序列$a_1,…,a_0\in\Sigma\cup\{\varepsilon\}$看起来没有任何意义 — 但实际上如果你说明它是一个空序列就有意义了。这里的条件$w=a_1\cdot\cdot\cdot a_0$,指代的是一个空序列或者空字符串的凭借,它的意思是$w=\varepsilon$。至于条件对于每个$k\in\{0,…,m-1\}$有$r_{k+1}\in\delta(r_k,a_{k+1})$成立是一个空洞的语句,因此它肯定是真的,因为没必要担心k的值。
这样,如果这种情况下假设NFA的初始状态$q_0$是可接受的,我们的输入使空字符串,那么NFA接受了输入 — 我们让$m=0$和$r_0=q_0$,这样就满足了定义。注意当一个DFA接受输入时,我们也可以在定义中做类似的事情:如果我们允许定义的第二个语句中的$n=0$,对于第一个语句来说是等价的,所以我们不需要分开处理这两种可能性。
类似于我们对DFA所做的,我们可以为NFA的转移函数定义一个扩展版本。特别是,如果
是一个NFA的转移函数,我们定义一个如下的
新函数。首先,我们定义一个任意集合$R\subseteq Q$的$\varepsilon$-闭包
另外一种定义$\varepsilon(R)$的方式是所有子集$T\in Q$的交集,它满足这些条件:
- $R\subseteq T$.
- 对于每个$q\in T$有$\delta(q,\varepsilon)\subseteq T$.
我们可以说明这个可供选择的定义表示$\varepsilon(R)$是$Q$的包含$R$的最小子集,并且你无法通过$\varepsilon$-转移跳出这个集合。
有这个$\varepsilon$-闭包的概念在手,我们递归地定义$\delta^{*}$如下:
- 对于每个$q\in Q$有$\delta^{*}(q,\varepsilon)=\varepsilon(\{q\})$,
- 对于每个$q\in Q、a\in\Sigma、w\in\Sigma^{*}$有$\delta^{*}(q,wa)=\varepsilon\Big(\bigcup_{r\in\delta^{*}(q,w)}\delta(r,a)\Big)$。
直观上来说,$\delta^{*}(q,w)$是你从状态$q$读取$w$做任意次$\varepsilon$-转移后可能到达的所有状态的集合。称一个NFA $N=(Q,\Sigma,\delta,q_0,F)$接受字符串$w\in\Sigma^{*}$等同于条件$\delta^{*}(q_0,w)\cap F\neq\varnothing$。
还有和DFA类似的是,$L(N)$表示NFA $N$所识别的语言:
NFA和DFA的等价关系
看起来NFA可能比DFA更强大,因为NFA有使用不确定性的选择。大概你已经在以前的课程中学习过,但接下来的理论声明会有所不同。
定理3.3. $\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个语言。语言$A$是正则的当且仅当对于某个NFA $N$有$A=L(N)$。
我们开始对这个定理进行拆分,看看能列出来那些需要证明的。 首先,看到“当且仅当”的陈述,所以这里有两件事需要证明:
- 如果$A$是正则的,那么对于某个NFA $N$有$A=L(N)$。
- 如果对于某个NFA $N$有$A=L(N)$,那么$A$是正则的。
如果你需要从中选一个出来先证明,选择第一个是很明智的:它是两个语句中较简单的。特别是,假设$A$是正则的,所以根据定义存在一个DFA $M=(Q,\Sigma,\delta,q_0,F)$可以识别A。我们的目标是定义一个NFA $N$也能识别$A$。着很简单,我们选取$N$作为这个NFA,它的状态图和$M$一样。正式水平上来看,$N$不完全和$M$一样;因为$N$是一个NFA,它的转移函数的形式与DFA的不同,但在这种情况下不同之处仅在表面。更正式地说,我们可以定义一个$N=(Q,\Sigma,\mu,q_0,F)$,它的转移函数$\mu:Q\times(\Sigma\cup\{\varepsilon\})\rightarrow\mathcal{P}(Q)$的定义对于所有的$q\in Q$和$a\in\Sigma$有
到这里我们得到$L(N)=L(M)=A$,证明就完成了。
现在我们考虑上面列的第二个语句。我们假设对于某个NFA $N=(Q,\Sigma,\delta,q_0,F)$有$A=L(N)$,我们的目标是说明$A$是正则的。也就是我们一定要证明存在一个DFA $M$使得$L(M)=A$。最直接的方式就是讨论,通过使用$N$的描述,我们可以提出一个等价的DFA $M$。如果我们能说明如何使用任意一个NFA $N$来定义一个DFA $M$使得$L(M)=L(N)$,那么这个证明就完成了。
我们将会使用NFA $N$的描述来定义一个等价的DFA $M$,通过一个简单的想法:每个$M$的状态都记录着一个$N$的状态子集。在读取输入字符串的任意部分后,总会有一些$N$可能处于的状态子集,然后我们将$M$设计成在读取字符串的任意部分后,它的状态就是$N$所对应的状态子集。
一个简单的例子
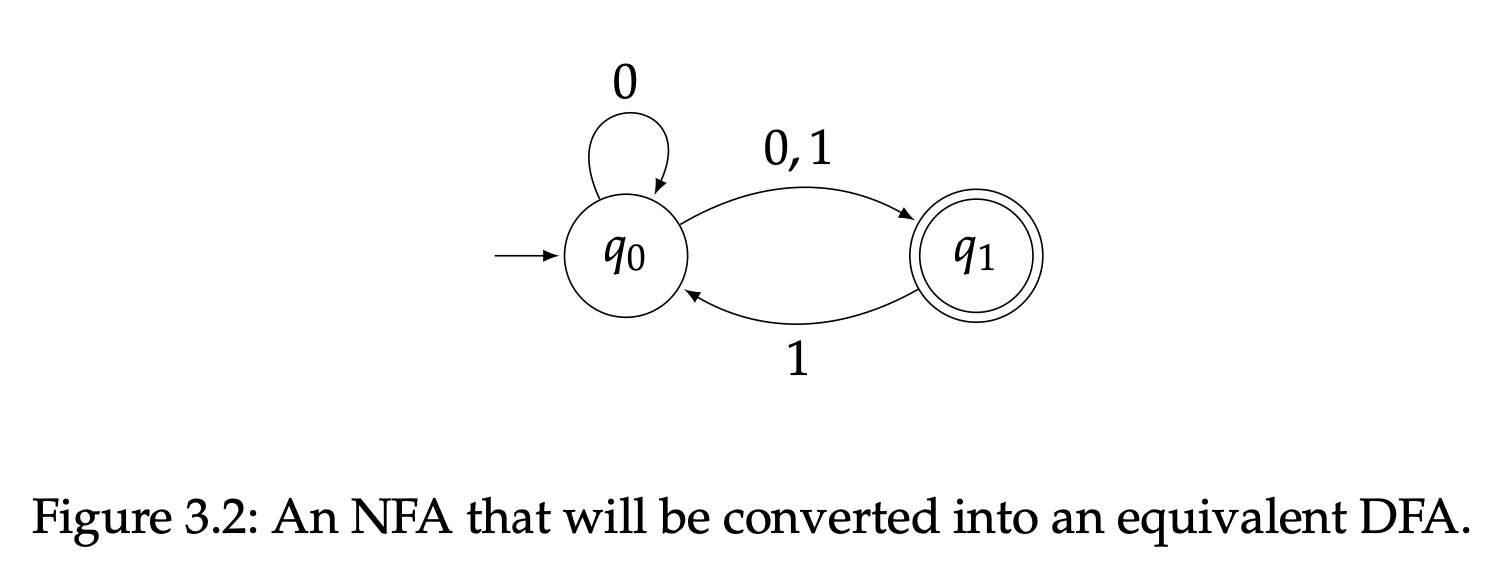
在我们详细描述之前,先来看一个简单的例子。已知一个NFA $N$如图3.2所示。如果我们根据定义正式地描述这个NFA,那就是
其中$Q=\{q_0,q_1\}、\Sigma=\{0,1\}$,以及$\delta:Q\times(\Sigma\cup\{\varepsilon\})\rightarrow\mathcal{P}(Q)$,定义如下:
我们将要定义个DFA $M$,对于每个$N$的状态集合他都有一个状态。我们可以根据自己的喜好来命名这些状态,也可以直接使用$Q$子集来表示。换句话说,$M$的状态集合就是幂集$\mathcal{P}(Q)$。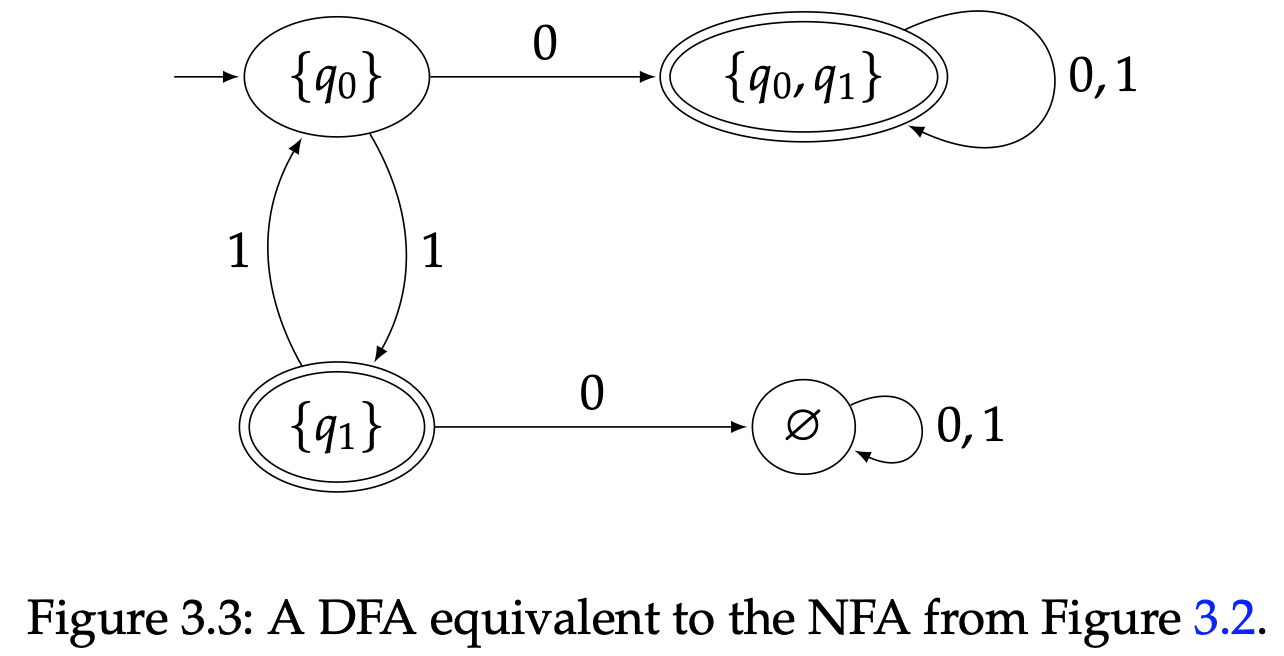
看一下状态图3.3,然后想一下如果它是$M$的有意义的不错选择。正式地讲,这个DFA就是
它的转移函数$\mu:\mathcal{P}(Q)\times\Sigma\rightarrow\mathcal{P}(Q)$的定义是
你们可以一步一步地验证一下这个DFA描述。
例如,假设某个时间点$N$处于状态$q_0$。如果读取了一个0,它既可以通过自循环保持状态$q_0$,也可以通过其他转移到$q_1$。这就是为什么在$M$中$\{q_0\}$输入0的转移是$\{q_0,q_1\}$;在$M$中的状态$\{q_0,q_1\}$代表着$N$可以处以$q_0$或者$q_1$中的任意一个状态。另外,如果$N$处于状态$q_1$读取了一个0,它却没有转移状态,这就是为什么在$M$中状态$q_1$标有0的转移状态是$\varnothing$。$M$中的状态$\varnothing$表示在$N$中没有状态转移(这是合理的,因为$N$是一个NFA)。状态$\varnothing$的自循环,不管输入是0还是1,表示如果在一个已知时刻$N$不处于任何状态,并且有一个符号被读取了,那它仍然不处于任何状态。你可以仔细检查其他的转移,用同样的方式验证它们。
还有一个问题是$M$中那些状态是接受状态。这部分很简单:我们让$M$的初始状态对应上$N$中我们不需要读取符号就已经处于的状态,在我们的例子中就是$\{q_0\}$,我们让$M$的接受状态对应上那些至少包含了$N$的$F$中一个状态的状态子集。
普遍结构
现在让我们从更广泛的角度来考虑上述建议。那就是我们会制定一个DFA $M$,对于任意一个NFA
它满足$L(M)=L(N)$。有一件事我们需要记住,$N$可以有$\varepsilon$-转移,然而我们的例子却没有。然而这会出现的,通过参考前面讨论的$\varepsilon$-闭包的概念,我们很容易处理$\varepsilon$-转移。另外一件需要谨记的事情是$N$确实是任意的 — 也许它由1000000个状态或者更多。因此我们很难用状态图来描述,所以我们将会抽象地解决这些问题。
首先,我们知道基于上述讨论$M$的状态集合是什么:$Q$的幂集$\mathcal{P}(Q)$。当然字母表$\Sigma$和$N$是一样的。因此为了保持这些选择一致,$M$的转移函数形式为
为了更精确地定义转移函数$\mu$,我们必须制定一个输出子集
其中每个子集$R\subseteq Q$以及每个符号$a\in\Sigma$。还有一种表示方式:
用文字来描述,等式的右边代表着在$N$中从$R$的任意一个状态通过标有a的转移,再经过任意次数的$\varepsilon$-转移能到达的每个状态。
最后我们需要做的事情是定义$M$的初始状态和接受状态。初始状态就是$\varepsilon(\{q_0\})$,也就是$q_0$通过$\varepsilon$-转换能到达的每个状态,而接受状态就是$Q$的子集,它至少包含了一个$N$的接受状态。如果我们用$G\subseteq\mathcal{P}(Q)$来表示$M$的接受状态集合,那么这个集合的定义是
DFA $M$可以正式指定为
现在,如果我们坦诚一点,就不能说我们已经证明了对于每个NFA $N$存在一个等价的MFA $M$满足$L(M)=L(N)$。我们所做的只是根据已知的NFA $N$定义一个DFA $M$,看起来像是满足了等价关系,事实上,$L(M)=L(N)$是对的,但我们不会正式证明。然而重要的是思考如果有必要我们应该怎么做。
首先,如果我们要证明两个语言$L(M)$和$L(N)$是相等的,最自然的方式就是把它拆分成两个语句:
- $L(M)\subseteq L(N)$.
- $L(N)\subseteq L(M)$.
这就是我们通常证明两个集合相等的方式。没人告诉我们,这两个语句需要用同样的方式证明,通过分开处理我们能有更多的选择。我们先从集合关系$L(N)\subseteq L(M)$开始,它等同于如果$w\in L(N)$,那么$w\in L(M)$。我们回到$N$接受字符串$w$的定义,并尝试得出$M$也必须接受$w$。把所有细节都写下来太繁琐了,但你可以说服自己相信它就是这样的。另外一个关系$L(M)\subseteq L(N)$等同于说如果$w\in L(M)$,那么$w\in L(N)$。这里的基本思想是相似的,尽管特殊情况有点不同。这次我们从一个DFA的接受定义开始,对于$M$可行,然后在尝试推论$N$一定接受$w$。
另外一个证明这些语句的方式是使用函数$\delta^{*}$和$\mu^{*}$这是我们在讨论$\delta$和$\mu$所定义的。基于$w$的长度使用归纳法,可以证明
其中每个字符串$w\in \Sigma^{*}$以及每个子集$R\subseteq Q$。只要我们有这个,我们知道$\mu^{*}(\varepsilon(\{q_0\}),w)$包含在$G$中当且仅当$\delta^{*}(q_0,w)\cap F\neq\varnothing$,也就是说它等价于$w\in L(M)$当且仅当$w\in L(N)$。
无论哪种情况,你不会被要求去正式化和验证这个阶段提出的证明,你只需要思考一下它是如何完成的。
NFA转换DFA的过程
在本课程中典型的一种作业就是给出一个NFA,要求使用上述构造方法得出等价的DFA。这种机械化的作业不要求什么创造性,观察计算及执行的构造方法本身往后在本课程是很重要的,然而你们需要经手一些样例才能明白这些话。
如果你发现自己在动手实现这个结构,有必要指出的是你真的不需要写出每个$N$的状态子集然后再画箭头。$M$中的状态数量是$N$的指数级,有时候其中有些状态完全没有用 — 它们不可能从$M$的初始初始状态到达,他们只是对应了包含了$N$的初始状态的集合的$\varepsilon$-闭包,那么你只要画出你需要的新状态就好了。
然而最坏情况下,你确实需要所有这些状态。举个例子,对于任意正整数n,如果某个语言的一个$NFA$有n个状态,那么最小的DFA都有$2^n$个状态。所以,当NFA和DFA在相同的计算能力下,将一个NFA转换成DFA的转换成本非常大,相较于原来的NFA,DFA需要保留大量的状态。