前言
这节课我们会讨论正则运算和正则表达式,以及它们和正则语言之间的关系。
知识点
正则运算
正则运算是用于语言的三种操作,下面的定义会解释清楚。
定义4.1. 已知$\Sigma$表示一个字母表,$A,B\subseteq \Sigma^{*}$表示语言。以下就是正则运算:
- Union(并集)。语言$A\cup B\subseteq\Sigma^{*}$的定义是用文字表达就是两个集合的并集,只是将集合换成语言而已。
- Concatenation(拼接)。语言$AB\subseteq\Sigma^{*}$的定义是用文字表达,这个语言包含了每个A中的字符串拼接上每个B中的字符串获得的所有字符串,并且A中的字符串在左边,而B中的字符串在右边。(注意,对于字符串$wx$的形式没有标记说明$w$在哪儿结束以及$x$在哪儿开始;它仅仅是将$w$和$x$放在一起的符号序列)
- Kleene star(克林星,或者简称星)。语言$A^{*}$的定义是用文字表达,$A^{*}$就是从$A$中选取任意有限数量的字符串拼接而成的字符串所组成的语言。(这包括了不选取字符串,也就是空字符串)
注意正则运算(regular operations)与正则语言(regular languages)两个名字只是巧合。而且正则运算也确实和正则语言有着紧密的联系,只是名字的选取并没有什么数学意义。
正则运算下的正则语言闭包
接下来我们证明一个关联正则运算和正则语言的理论。
定理4.2. 对于正则语言的正则运算是封闭的:如果$A,B\subseteq \Sigma^{*}$是正则语言,那么语言$A\cup B、AB、A^{*}$也是正则的。
证明:首先我们观察到,因为$A$和$B$是正则的,所以存在DFA
使得$L(M_A)=A$和$L(M_B)=B$。接下来我们的证明需要用到这些DFA。因为我们可以在不影响语言识别的情况下自由命名状态,假设$P和Q$是不相交集合不会失去普遍性(这意味着$P\cap Q=\varnothing$)。
让我们从$A\cup B$开始。从上一节课中我们知道如果存在一个NFA $N$使得$L(N)=A\cup B$,那么$A\cup B$则是正则的。记住这一点,我们的目标就变成了定义这样一个NFA。我们将会定义这个NFA $N$,它的状态包含了$P$和$Q$的所有元素,同时还包含一个既不属于$P$也不属于$Q$的状态$r_0$。这个新状态$r_0$是$N$的初始状态。然后定义$N$的转移函数,$P$中所有的状态转移函数是$\delta$和$Q$中所有状态的转移函数$\mu$都是已知的,再加上两个$\varepsilon$-转移,一个是从$r_0$到$p_0$,另一个是从$r_0$到$q_0$。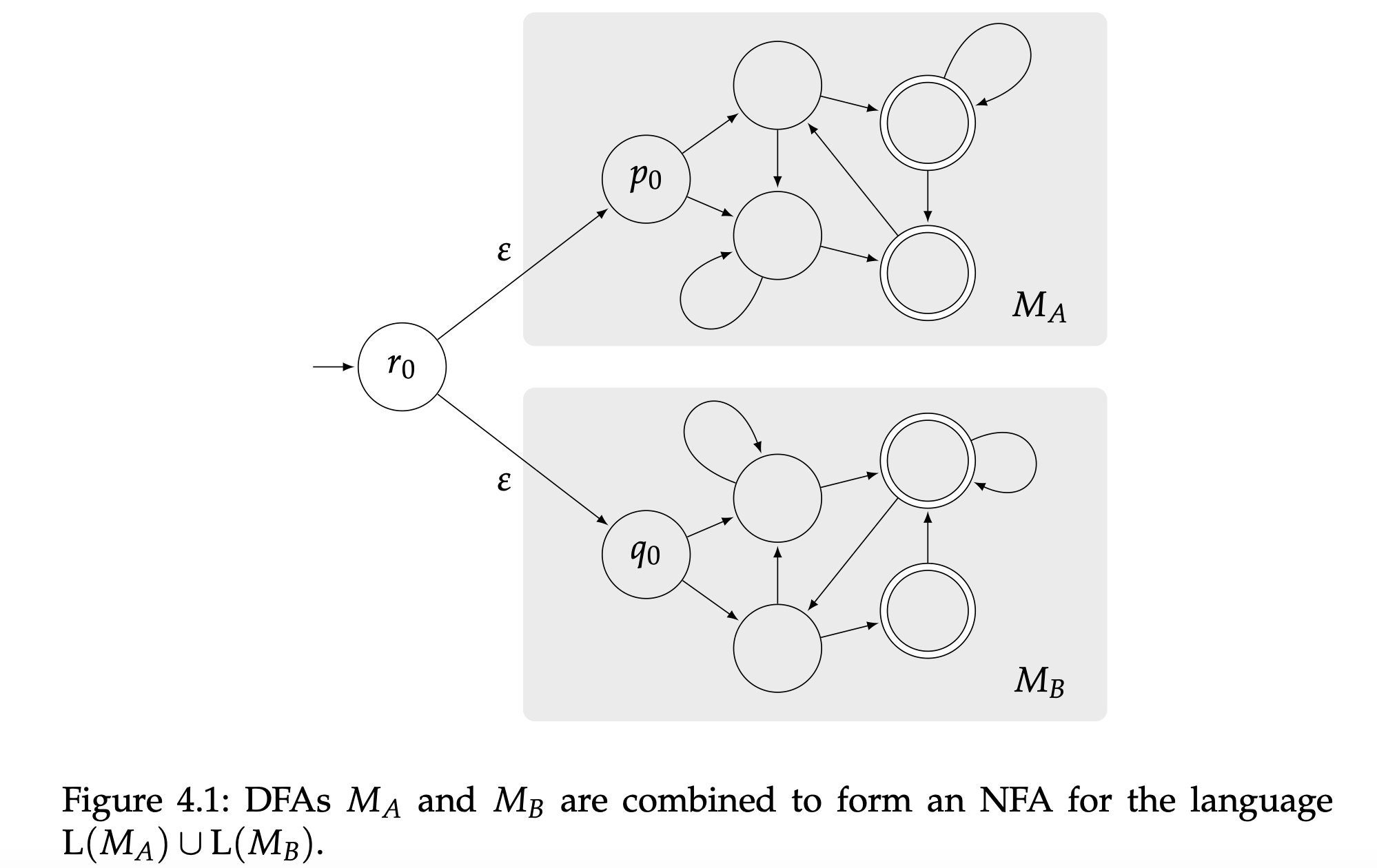
图4.1展示NFA $N$状态图概况。你应该将标有$M_A$和$M_B$的阴影方框想象为$M_A$和$M_B$的状态图。(图中的两个DFA是假设的,$M_A$和$M_B$的真实状态图当然是任意的)
我们正式指定$N$如下:
其中$R=P\cup Q\cup\{r_0\}$(在我们的假设中$P,Q,\{r_0\}$是不相交集合)和转移函数
的定义如下:
$N$的接受状态实是$F\cup G$。
每个能被$M_A$接受的字符串也能被$N$接受,因为我们可以采用一个步从$r_0$到$p_0$的$\varepsilon$-转换,接下来的转移就和$M_A$一样了。同样的道理每个能被$M_B$接受的字符串也能被$N$接受。最后每个能被$N$接受的字符串都能被$M_A$或者$M_B$接受(或者同时接受),因为每个被接受的计算都是以两个$\varepsilon$-转换之一开始的,然后由此决定采用$M_A$或者$M_B$的接受计算。因此也就有了
我们得出$A\cup B$是正则的。
下一步我们证明$AB$是正则的。思路和上面一样:我们理由DFA $M_A$和$M_B$定义一个语言$AB$的NFA $N$。这次$N$的状态集合是并集$P\cup Q$,$M_A$的初始状态$p_0$将会是$N$的初始状态,另外我们还要给每个$M_A$的接受状态添加一个$\varepsilon$-转换到$M_B$的初始状态。最后,$N$的接受状态就是$M_B$的接受状态$G$。图4.2展示了基于$M_A$和$M_B$的$N$结构。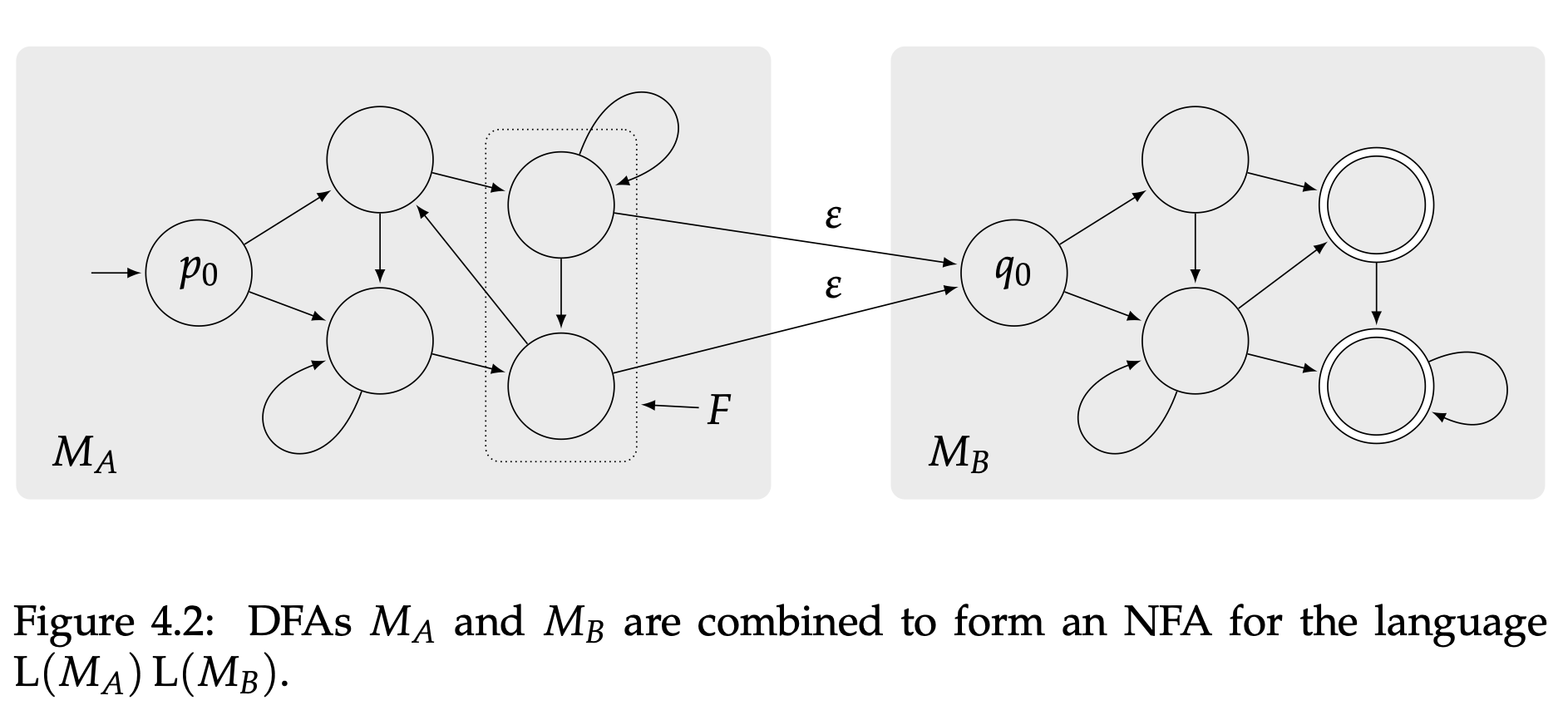
使用正式术语,NFA $N$的定义是
其中转移函数
的定义是
和我们前面证明$A\cup B$是正则的一样,你们可以论证$N$识别语言$AB$,由此腿短$AB$是正则的。
最后我们将要证明$A^{*}$是正则的,证明过程也是类似的。但这次我们只考虑$M_A$,因为语言$B$并不涉及其中。这次我们直接正式指定$N$;定义是
其中$R=P\cup\{r_0\}$以及转移函数
的定义是
用文字描述,$N$的状态就$M_A$的状态加上一个$r_0$,而$r_0$即是初始状态也是接受状态。而$N$的转移包含了所有$M_A$的转移,加上从$r_0$到$M_A$初始状态$p_0$的$\varepsilon$-转移和从$M_A$的接受状态回到$r_0$的$\varepsilon$-转移。图4.3展示了$N$和$M_A$的关系。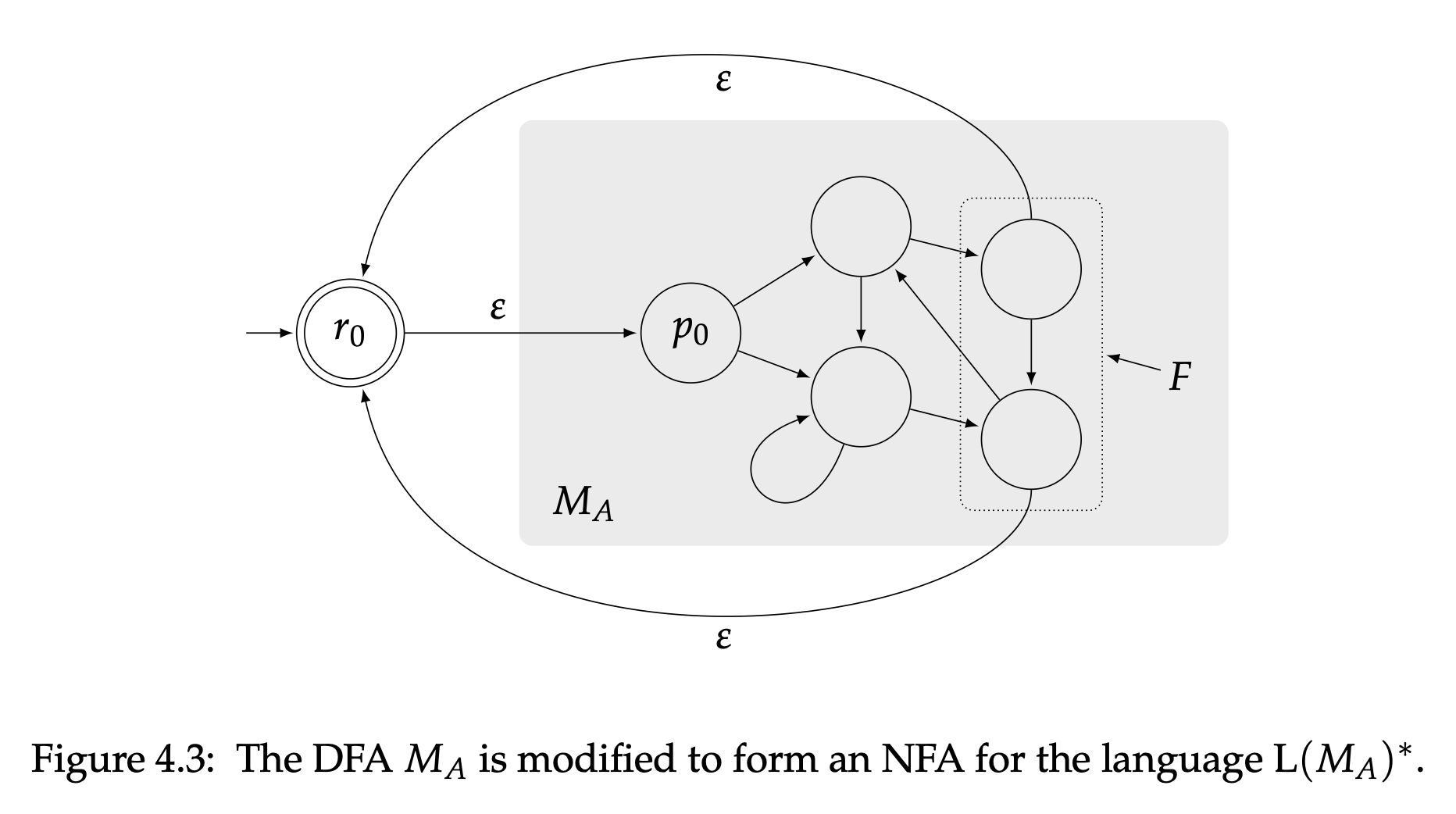
很明显$N$可以识别语言$A^{*}$。这是因为所有这些字符串明确导致了$N$从状态$r_0$出发后又回到$r_0$零次或者多次,每次循环都对应这个某个可以被$M_A$接受的字符串。当$L(N)=A^{*}$,也就得出$A^{*}$是正则的,如此证明就完成了。
很自然我们会想到为什么不用并集和拼接操作来证明$A^{|*}$是正则的。具体一点,我们有
很简单可以看出语言$\{\varepsilon\}$是正则的 — 这里有一个识别语言$\{\varepsilon\}$的NFA(对于任意字母表):
语言$\{\varepsilon\}\cup A$是正则的,因为两个正则语言的并集也是正则的。我们也知道$AA$是正则的,因为两个正则语言的拼接也是正则的。依次类推我们会发现语言
是正则的,语言
也是正则的,等等都是如此。是不是这就意味着$A^{*}$正则呢?
答案是“不是”。尽管只要$A$是正则的,$A^{*}$就是正则的,正如我们前面所证明的,但是仅靠并集和拼接却并不能证明它。这是因为我们不能从这个论证得出此无限集合是正则的,而只能得到有限集合是正则的。
如果你仍然怀疑或者不确定,考虑一下这个陈述:
如果A是一个有限语言,那么A*也是一个有限语言。
一般而言这个陈述是错的。比如,$A=\{0\}$是有限的,但是
是无限的。另外,的确两个有限语言的并集是有限的,并且两个有限语言的拼接还是有限的,所以当你将这些结论组合起来得出$A^{*}$是无限集合的时候,一定有什么地方出错了。当你将特性“有限”替换成“正则”后,情况也是一样的。
正则语言的其他特性闭包
对于闭合的正则语言,除了正则运算外还有很多其他运算。比如,一个正则语言的补集(complement)也是正则的。为了保证术语是清楚的,这里有语言补集的定义。
定义4.3. 已知$A\subseteq\Sigma^{*}$是一个基于字母表$\Sigma$的语言。$A$的补集,记作$\overline{A}$,是一个使用$\Sigma$中字母组成的所有不包含于A的字符串构成的语言:
命题4.4. 已知$\Sigma$是一个字母表,$A\subseteq \Sigma^{*}$是一个基于$\Sigma$的正则语言。语言$\overline{A}$也是正则的。
这个命题很容易证明:因为$A$是正则的,一定存在一个DFA $M=(Q,\Sigma,\delta,q_0,F)$使得$L(M)=A$。通过将交换$M$的接受和拒绝状态,我们就得到了$\overline{A}$的DFA。也就是DFA $K=(Q,\Sigma,\delta,q_0,Q\backslash F)$能够识别$\overline{A}$。
如果已知一个语言的DFA,通过交换接受和拒绝状态我们就能轻松获取它的补集语言的DFA,但是这个方法对于NFA无效。比如你也许能将一个NFA的接受和拒绝状态交换,但你得到的NFA能识别的却不是它语言的补集。这是因为非确定性模型的接受与拒绝的非对称性质。
接下来的课程中我们会看到闭合正则语言的运算的更多例子。这节课还有一个例子。
命题4.5. 已知$\Sigma$是一个字母表,$A$和$B$是基于$\Sigma$的正则语言。交集$A\cap B$也是正则的。
这次我们通过联合已知的闭包属性来证明。由德摩根定律可知
如果$A$和$B$是正则的,那么$\overline{A}$和$\overline{B}$就是正则的,因此$\overline{A}\cup\overline{B}$是正则的,又因为这个正则语言的补集是$A\cap B$,我们得到$A\cap B$是正则的。
这里有另一种方式可以证明$A\cap B$是正则的,它是可以直接论证的。因为语言$A$和$B$是正则的,一定存在DFA
使得$L(M_A)=A$和$L(M_B)=B$。我们使用笛卡尔积构造一个DFA $M$:
其中对于每个$p\in P、q\in Q、a\in\Sigma$有
本质上,DFA $M$就像是在同时运行$M_A$和$M_B$,接受时机当且仅当$M_A$和$M_B$同时接受。用同样的思路你也可以获得$A\cup B$的DFA(但是接受时机当且仅当$M_A$或者$M_B$接受)。
正则表达式
我希望你已经对正则表达式有过了解;它们在编程语言和其他指定模式的搜索和字符串匹配中应用广泛。当实际使用正则表达式时,我们代表性地赋予他们丰富的运算集合,但在这里我们仅采用最低限度的正则表达式定义,只允许三种正则运算(没有其他类似于否定运算或者标记输入的起始或者结束字符的特殊符号)
下面有我们将会采用的正则表达式的正式定义。这个定义是归纳定义的一个例子,有一些关于归纳定义的解释紧随其后。
定义4.6. 已知$\Sigma$是一个字母表。$R$是基于字母表$\Sigma$的正则表达式当且仅当它拥有以下性质中的任意一个:
- $R=\varnothing$.
- $R=\varepsilon$.
- 对于某个$a\in\Sigma$有$R=a$.
- 对于正则表达式$R_1$和$R_2$有$R=(R_1\cup R_2)$.
- 对于正则表达式$R_1$和$R_2$有$R=(R_1R_2)$.
- 对于正则表达式$R_1$有$R=(R_1^{*})$.
当你看到类似与这样的归纳定义,你应该用最通俗的方式来说明它,而不能把它看成是某种循环的或者似是而非的东西。比如,当我们看到对于任意任意正则表达式$R_1$有$R=(R_1^{*})$,这应该被理解为$R_1$已经是一个定义明确的正则表达式了。比如我们不能将$R_1$当做正则表达式$R$,否则我们将会得到$R=(R^{*})$,这将会被解释成一个奇怪的、分形表达式,看起来就是这样:
像这样的东西根本就不是一个正则表达式,根据定义的通俗解释这不是有效的。这里有一些基于二进制字母表$\Sigma=\{0,1\}$的有效正则表达式的例子:
当我们说到基于字母表$\Sigma$的正则表达式,你应该把他们想象成一个字符串,它基于字母表
(假设$\Sigma$和$\{(,),*,\cup,\varepsilon,\varnothing\}$不相交)。有些人会用不同的字体来写正则表达式,这样让它们看起来更明显,但我不会这样做(一部分原因是因为我的板书只有一种字体,另外就是我不认为那有必要)。
接下来我们将会通过一个已知的正则表达式定义识别语言(或者匹配)。这次又是递归定义,它和本身正则表达式的定义是直接并行的。如果它看起来像是在陈述一些显而易见的事情,那么你的感觉是对的;我们要求一个正式定义,但本质上说我们应该用最直接和自然的方式定义一个被正则表达式匹配的语言。
定义4.7. 已知$R$是一个基于字母表$\Sigma$的正则表达式。$R$的识别语言被记作$L(R)$,定义如下:
- 如果$R=\varnothing$,那么$L(R)=\varnothing$.
- 如果$R=\varepsilon$,那么$L(R)=\{\varepsilon\}$.
- 如果对于任意$a\in\Sigma$有$R=a$,那么$L(R)=\{a\}$.
- 如果对于任意正则表达式$R_1$和$R_2$有$R=(R_1\cup R_2)$,那么$L(R)=L(R_1)\cup L(R_2)$.
- 如果对于任意正则表达式$R_1$和$R_2$有$R=(R_1R_2)$,那么$L(R)=L(R_1)L(R_2)$.
- 如果对于任意正则表达式$R_1$有$R=(R_1^{*})$,那么$L(R)=L(R_1)^{*}$.
正则运算的优先级
在定义4.6的正则表达中我们看到了很多括号。比如正则表达式$(((0\cup\varepsilon)^{*})1)$的括号多于非括号的符号。括号保证了每个正则表达式的含义明确。
然而根据一种引入的正则运算优先级顺序,我们就不在需要这么多括号了。顺序如下:
- 星号(最高优先级)
- 拼接
- 并集(最低优先级)
为了更明确,我们不会改变正式定义中的正则表达式,只是引入一种约定允许一些括号被省略,这会让正则表达式看起来更简单。比如,我们会写
而不是
认同以上优先级顺序后,看起来简单的正则表达式就被视为第二表达形式。
一种简单的记忆优先级顺序的方式就是将它们类比于你所熟知的代数运算:星号看起来求幂,拼接看起来像乘法,并集就像加法。所以就像表达式$xy^2+z$与$((x(y^2))+z)$有相同的含义,表达式$10^{*}\cup 1$和$((1(0^{*}))\cup 1)$也一样。
正则表达式描述正则语言
到了这个点上很自然会想到哪些语言有正则表达式。答案是具有正则表达式的语言类就是正则语言类。(如果不是你就会想为什么正则语言这样命名。注:正则语言的英文名是regular languages,正则表达式的英文名是regular expressions)
要确定正则语言和具有正则表达式的语言是一致的,需要考虑两个问题。让我们从第一个开始,他的内容就是下面这个命题。
命题4.8. 已知$\Sigma$是一个字母表,$R$是一个基于字母表$\Sigma$的正则表达式。语言$L(R)$是正则的。
证明这个命题的思路很简单:我们可以轻松的构造基于语言$\varnothing$、$\{\varepsilon\}$、$\{a\}$(对于任意符号$a\in\Sigma$)的DFA,通过重复使用定理4.2的结构,我们可以联合这些DFA构造一个NFA,它能识别同样具有这种语言的任意正则表达式。
另外一个问题的内容是下面这个定理,它上面这个证明起来要难一些。要是你感兴趣的化我已经提供了一个证明,不然你可以跳过它;这堂课的考试或者家庭作业中不会要求你学习这个证明。
定理4.9. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个正则语言。存在一个基于字母表$\Sigma$的正则表达式使得$L(R)=A$。
证明:因为$A$是正则的,一定存在一个DFA $M=(Q,\Sigma,\delta,q_0,F)$使得$L(M)=A$。我们可以自由使用任意名称来代表DFA的状态,所以假设对于某个正整数$n$有$Q=\{1,…,n\}$不会失去普遍性。
我们现在将要定义一种语言$B_{p,q}^k\subseteq\Sigma^{*}$,其中状态$p,q\in\{1,…,n\}$和整数$k\in\{0,…,n\}$。语言$B_{p,q}^k$所有字符串$w$的集合,$w$导致$M$的运行如下:
如果我们让$M$从状态$p$开始,那么读取$w$使得$M$转移到状态$q$。此外,除了初始状态$p$和结束状态$q$,当DFA $M$这样读取$w$时只经过了集合$\{1,…,k\}$中的状态。
比如,语言$B_{p,q}^n$中的所有字符串造成了$M$从状态$p$到$q$(此处限制中间状态没任何意义了)。在另一种极端情况下,集合$B_{p,q}^0$一定是一个有限集合;如果没有从$p$到$q$的直接转移,它可能是一个空集,在$p=q$的情况下它不包含任何字符串,通常它包含长度为1的字符串,这些字符串所对应的字符导致$M$从$p$转移到$q$。
现在我们将会对于k做归纳来证明存在一个正则表达式$R_{p,q}^k$使得$L(R_{p,q}^k)=B_{p,q}^k$,其中$p,q\in\{1,…,n\}$和$k\in\{0,…,n\}$。基本情况是$k=0$。对于每一对$p,q\in\{1,…,n\}$语言$B_{p,q}^0$是有限的,包含的字符串长度是0或者1,所以可以直接定义一个对应的正则表达式$R_{p,q}^0$匹配$B_{p,q}^0$。
至于归纳步骤,我们假设$k\geq 1$,并且存在一个正则表达式$R_{p,q}^{k-1}$使得对于每一对$p,q\in\{1,…,n\}$有$L(R_{p,q}^{k-1})=B_{p,q}^{k-1}$。有这样一种情况
这个等价关系反映了通过状态集合$\{1,…,k\}$导致$M$从$p$到$q$的字符串要么没有经过状态$k$,要么经过了状态$k$一次或者多次。因此我们可以定义一个正则表达式$R_{p,q}^k$使得对于每一对$p,q\in\{1,…,n\}$有$L(R_{p,q}^k=B_{p,q}^k$如下
最后,我们获得了一个正则表达式$R$满足$L(R)=A$,定义是
(用文字表达,$R$是所有正则表达式$R_{q_0,q}^n$的并集,其中$q$是一个接受状态)如此证明就完成了。
有一种程序可以将一个已知的DFA转换成一个等价的正则表达式。这个转换的思路就类似于我们上面的证明。一个相对简单地DFA可能会生成一个巨大且复杂的正则表达式,但它的确是有效的 — 就像将一个NFA转换成等价的DFA,它可以通过计算机来实现。