John Watrous 《Introduction to the Theory of Computing》08 -- 分析树、歧义性和乔姆斯基范式

前言

这节课我们会讨论一些有关于上下文无关语法的重要概念，包括分析树、歧义性，还有一种特殊形式的上下文无关语法，被称为乔姆斯基范式。

知识点

最左侧推导和分析树

上一节课中我们降到了上下文无关语法的定义以及通过上下文无关于的字符串推导。让我们考虑上节课中的一个上下文无关语法：

$$S\rightarrow 0S1S\ |\ 1S0S\ |\ \varepsilon\tag{8.1}$$

这次我们称这个CFG为$G$，正如我们上次证明的，我们得到

$$L(G)=\{w\in\Sigma^{*}:|w|_0=|w|_1\},\tag{8.2}$$

其中$\Sigma=\{0,1\}$是一个二进制字母表，$|w|_0$和$|w|_1$表示符号0和1分别在$w$中出现的次数一样。

最左侧推导

这里有一个字符串$0101$的推导样例：

$$S\Rightarrow 0S1S\Rightarrow 01S0S1S\Rightarrow 010S1S\Rightarrow 0101S\Rightarrow 0101.\tag{8.3}$$

这是一个最左侧推导的样例，意思是每次都是从最左侧的变量开始替换。对于第一步，只存在一个可被替换的变量；不管是在这个例子中还是在普遍情况下都是这样的。然而第二步中我们就可以选择任意一个$S$来替换，在上面的推导中就是最左侧的那个被替换了。如果我们把替换前和替换后的部分画上下划线，就是这样的：

$$0\underlineline{S}1S\Rightarrow 0\underline{1S0S}1S.\tag{8.4}$$

没有每个其他的步骤也是一样的：总是选择出现在最左侧的变量进行替换，这就是为什么我们称它为最左侧推导。同样的术语也普遍适用于任意上下文无关语法。
　　如果你多想一会儿，你会很快发现每个能被某个指定上下文无关语法生成的字符串，也能被同样的语法通过最左侧推导生成。这是因为在任意上下文无关语法的推导中，多个变量和符号之间没有“相互影响”；如果我们知道哪条规则可以用来替换每个变量，那么采用何种顺序来替换并没有什么影响，所以你也许可以在每一步中都总是选择最左侧变量。
　　我们也可以定义一个最右侧推导的定义，也就是每次总是计算最右侧的变量，但是这个最右侧推导并没有重要价值，至少在本课程中它完全可以用最左侧推导。由于这个原因，我们不在对最右侧推导进行更进一步的讨论了。

分析树

对于任意通过上下文无关语法的字符串推导，我们可以将它和一棵树关联起来，叫做分析树，它遵从以下规则：

1. 对于每个新出现的变量、符号或者$\varepsilon$都有一个节点，根节点则对应着初始变量。我们仅当有形式为$V\rightarrow \varepsilon$的规则被使用时才会有标记了$\varepsilon$的节点。
2. 每个对应着符号或者$\varepsilon$的节点都是一个叶子节点，而每个对应着变量的节点都有它被替换后对应着的符号、变量或者$\varepsilon$的孩子节点。每个变量被替换后的孩子的顺序和替换这个变量所使用的的规则中的变量和符号的顺序相同。

比如，推导（8.3）产生的分析树如图8.1。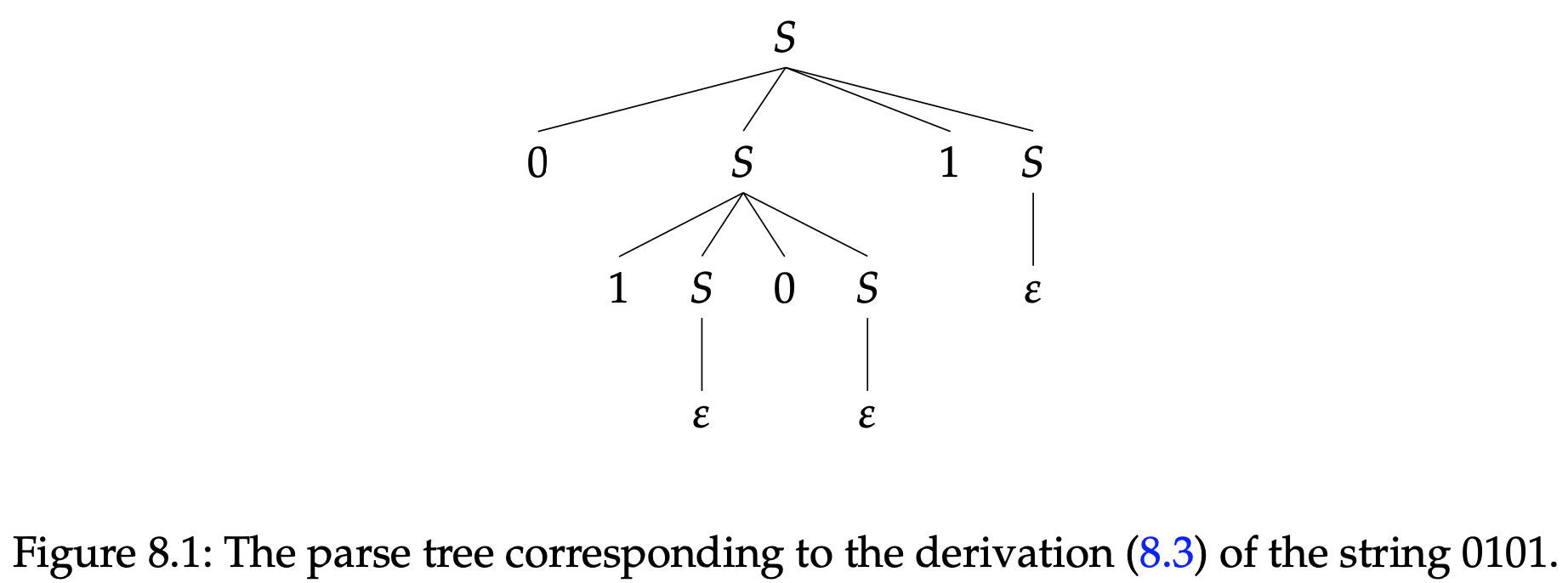

这里分析树和最左侧推导之间是一个单射且满射的对应关系，它意味着每个分析树唯一确定了一个最左侧推导并且每个最左侧推导唯一确定了一个分析树。

歧义性

有时候一个上下文无关语法允许它所生成的某个字符串有多个分析树。比如，由图8.1的CFG通过最左侧推导生成的字符串$0101$，字符串$0101$通过CFG最左侧推导还有一种不同于（8.3）方式是

$$S\Rightarrow 0S1S\Rightarrow 01S\Rightarrow 010S1S\Rightarrow 0101S\Rightarrow 0101.\tag{8.5}$$

这个推导对应的分析树如图8.2所示。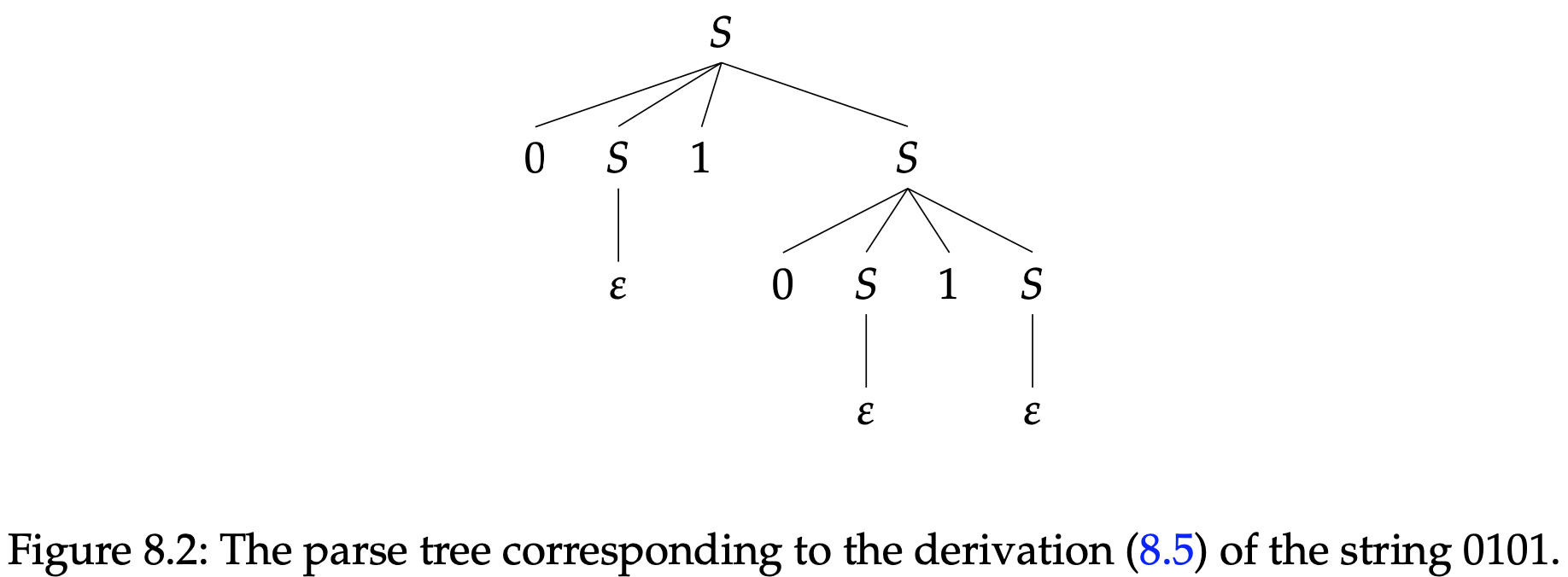

　　在这种情况下，对于一个已知的上下文无关语法$G$，至少有一个字符串$w\in L(G)$至少有两个不同的分析树，那么CFG $G$就是有歧义的。即使只有一个字符串拥有多个分析树也是如此；为了消除歧义，一个CFG对于每个它所生成的字符串只能有一个唯一的分析树。
　　消除歧义已经普遍被当做是一个CFG的积极性质，而且这也是某些上下文无关语法应用的明确要求。

设计无歧义的CFG

在某些情况下，一个无歧义的语法生成的语言和一个有歧义的语法生成的语言是一样的。比如，我们可以为（8.2）的语言$L(G)$提出一个不同的上下文无关语法，和CFG（8.1）不同，这个语法是无歧义的。这个语法是这样的：

$$\begin{align}&S\rightarrow 0X1S\ |\ 1\Upsilon0S\ |\ \varepsilon \\ &X\rightarrow 0X1X\ |\ \varepsilon \\ &\Upsilon\rightarrow 1\Upsilon 0\Upsilon \ |\ \varepsilon\end{align}\tag{8.6}$$

我们不会花时间来证明这个CFG是无歧义的了，如果你多想一会儿应该能够说服自己它确实是无歧义的。变量$X$生成的字符串中的0和1的数量相同，当你从左往右读的时候1的数量绝对不会超过0的数量，至于变量$\Upsilon$也是类似的，只不过0和1的顺序反过来了。如果你尝试用这个语法通过最左侧推导生成指定的字符串，每次不会有超过一条规则供你采用。
　　另外有一个例子讲解如何将一个有歧义的语法修改为无歧义的。让我们定义一个字母表

$$\Sigma=\{a,b,+,*,(,)\}\tag{8.7}$$

以及一个CFG

$$S\rightarrow S+S\ |\ S*S\ |\ (S)\ |\ a\ |\ b.\tag{8.8}$$

这个语法生成的字符串就像一个算数表达式，其中变量是$a$和$b$，我们允许的运算符是$*$和$+$，还有括号。
　　例如，字符串$(a+b)* a+b$对应着一个表达式，这个字符串的一个推导如下：

$$\begin{align}S\Rightarrow S*S &\Rightarrow (S)*S\Rightarrow (S+S)*S\Rightarrow (a+S)*S\Rightarrow (a+b)*S \\ &\Rightarrow (a+b)*S+S\Rightarrow (a+b)*a+S\Rightarrow (a+b)*a+b.\end{align}\tag{8.9}$$

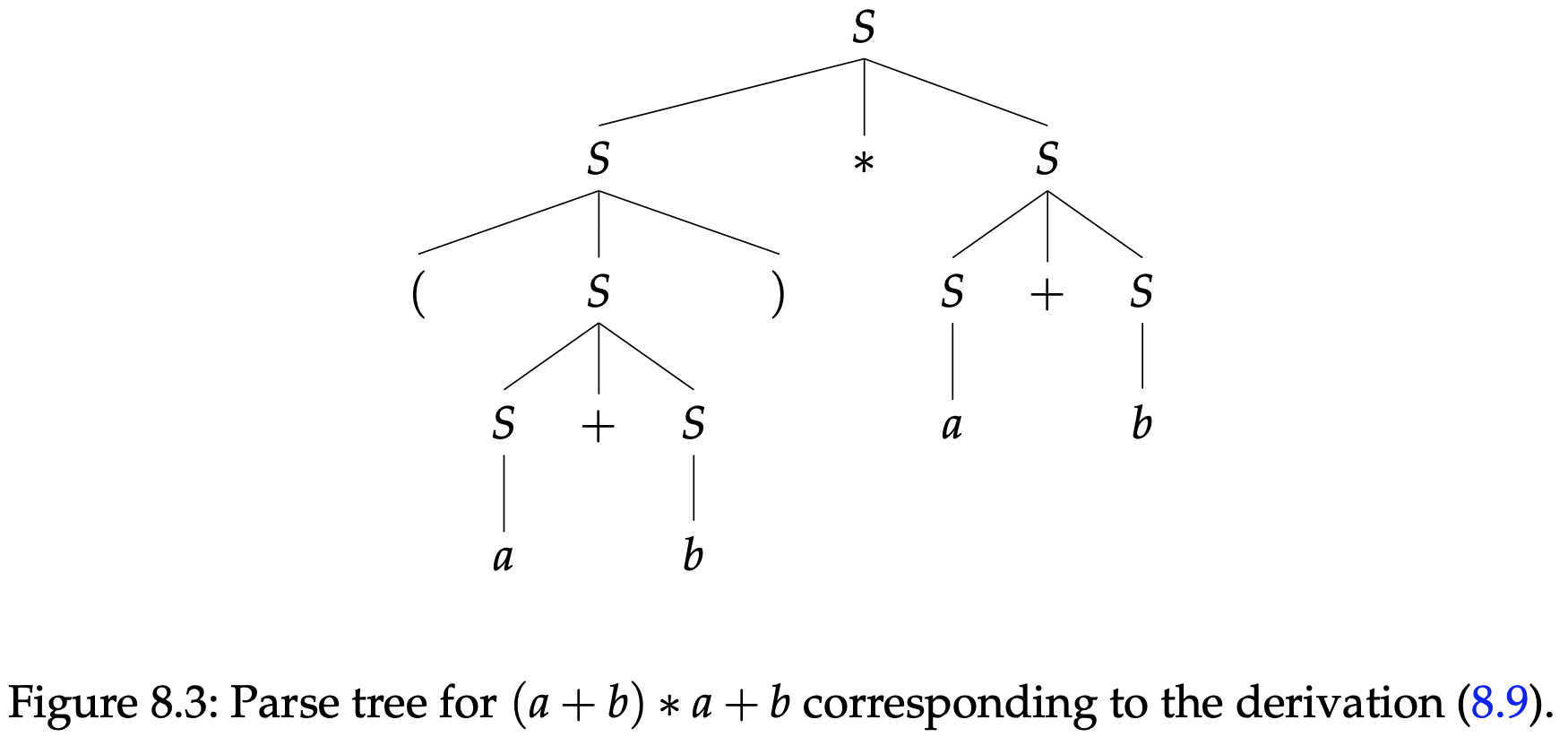
这是恰好是一个最左侧推导，因为每次都是最左侧的变量被替换。这个推导对应的分析树如图8.3所示。你当然可以构思一个此语法的更为复杂的版本，允许使用其他的算数运算符，变量等等，为了方便我们坚持使用（8.8）中的语法。
　　CFG（8.8）是有歧义的。例如，同样的字符串$(a+b)* a+b$还有一个不同的（最左侧）推导版本是

$$\begin{align}&S\Rightarrow S+S\Rightarrow S*S+S\Rightarrow (S)*S+S \\ &\Rightarrow (S+S)*S+S\Rightarrow (a+S)*S+S\Rightarrow (a+b)*S+S \\ &\Rightarrow (a+b)*a+S\Rightarrow (a+b)*a+b,\end{align}\tag{8.10}$$

这个推导的分析树如图8.4所示。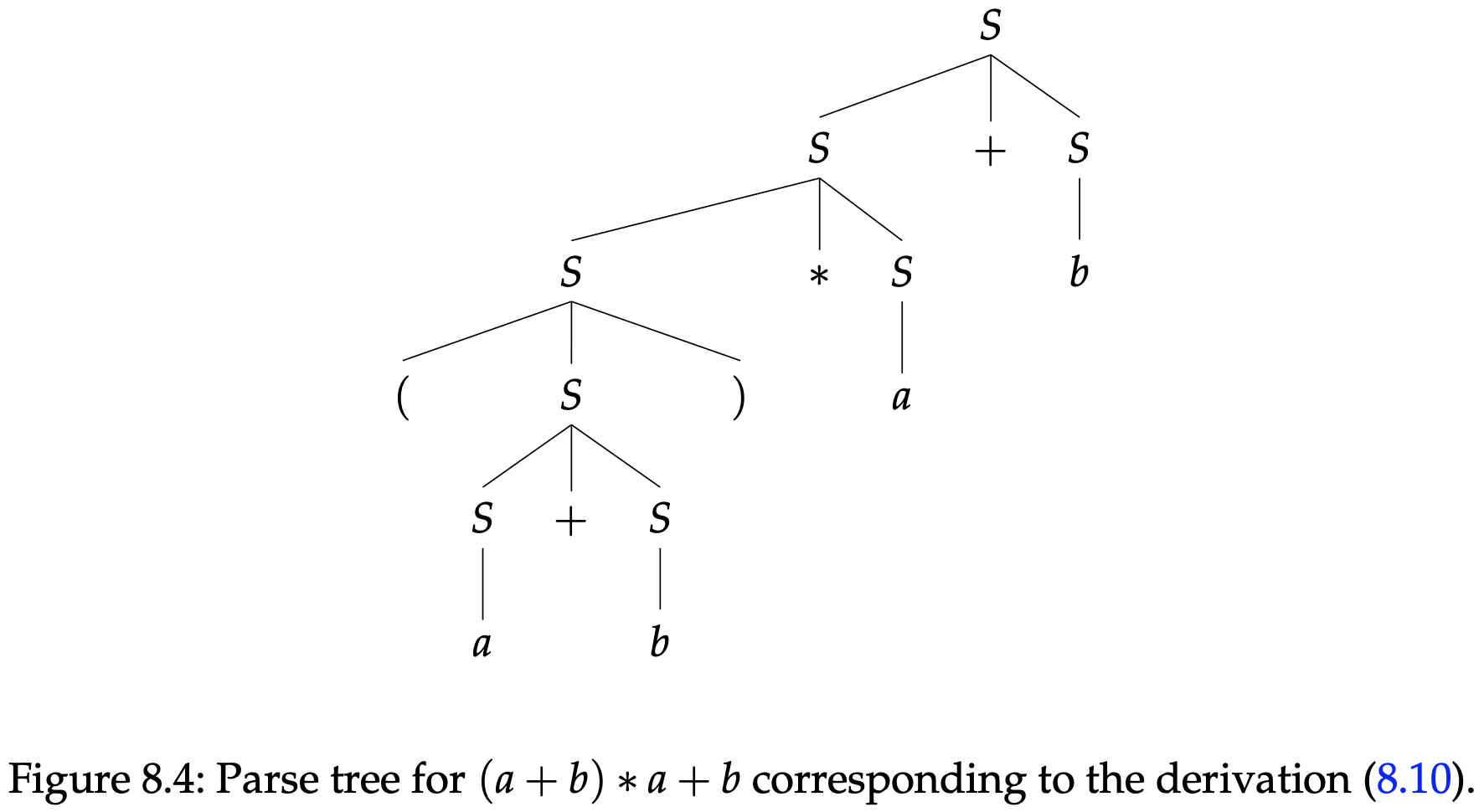

　　注意图8.4中的这个分析树是引人注目的，因为它实际解释了表达式$(a+b)* +b$的含义，从某种意义上来说，这个树反映了算术运算符的标准优先级顺序。想法，图8.3的分析树似乎是在表现一种加法比乘法优先级更高的运算。
　　语法（8.8）的歧义在某种情况是确实是个问题，它的分析树没有清楚表达我们刚才所描述的算数表达式。比如，如果我们设计一个编译器，并且想要使用这个语法来表达算数表达式（实际情况下要求的语法比这个更为复杂），（8.8）这个CFG完全就不适用。
　　然而对于同样的语言我们可以提出一个新的CFG，这个就好很多了，从某种意义上来说，它是无歧义的，并且抓住了算数表达式的正确含义（乘法的优先级高于加法）。它就是：

$$\begin{align}&S\rightarrow T\ |\ S+T \\ &T\rightarrow F\ |\ T*F \\ &F\rightarrow I\ |\ (S) \\ &I\rightarrow a\ |\ b.\end{align}\tag{8.11}$$

例如，字符串$(a+b)* +b$所对应的唯一分析树如图8.5所示。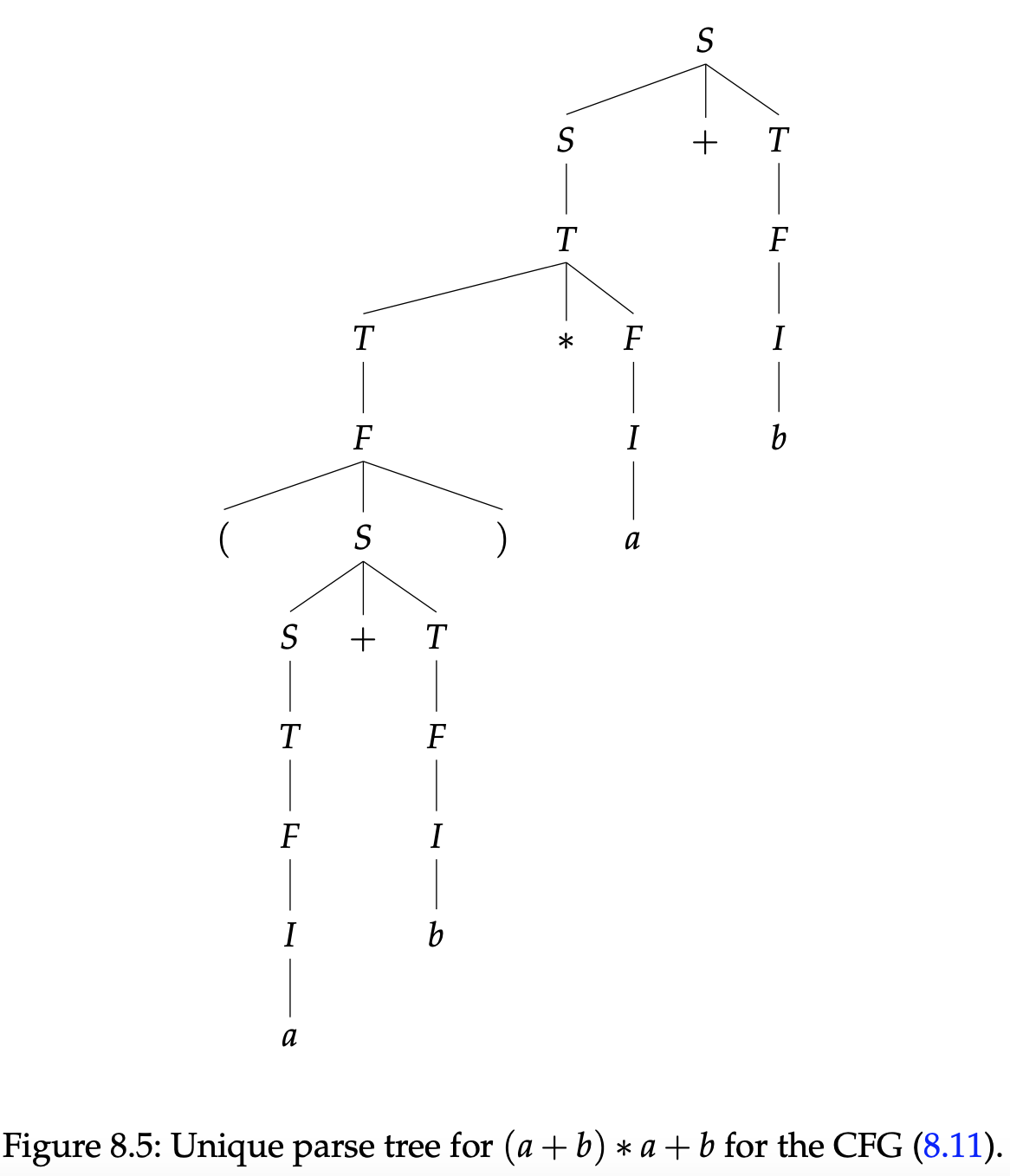

　　为了更好地理解CFG（8.11），关联不同变量的含义也许会有帮助。在这个CFG中，变量$T$生成项（terms），变量$F$生成因子（factors），然后变量$I$生成标识符（identifiers）。一个表达式不是一个项就是项之和，一个项不是一个因子就是因子的产物，一个因子不是一个标识符就是一个在括号内的完整表达式。

固有歧义性语言

当我们见过一个无歧义的CFG和一个有歧义的CFG可能会生成同样的语言后，但这种情况并不总是可能的。有一些上下文无关语言只能由有歧义的CFG生成。这种语言我们称为固有歧义性语言。举一个固有歧义性语言的例子就是：

$$\{0^n1^m2^k:n=m或者m=k\}.\tag{8.12}$$

我们不会证明这个语言是固有歧义性的，但是直觉告诉我们不管你想到什么CFG，对于足够大的$n$字符串$0^n1^n2^n$总会有多个分析树。

乔姆斯基范式

有些上下文无关语法很奇怪。例如，CFG

$$S\rightarrow SSSS\ |\ \varepsilon\tag{8.13}$$

简单地生成语言$\{\varepsilon\}$；但是他明显是有歧义的，而且更糟的是它所生成字符串$\varepsilon$有无限个分析树。如果我们知道不能成功消除一些CFG的歧义，那是因为这些上下文无关语言是固有歧义性的，我们甚至不能消除它对于已知字符串拥有无限个分析树的可能性。也许更重要的是，对于任意已知CFG $G$，我们总会提出一个新的CFG $H$使得$L(H)=L(G)$，我们保证每个已知字符串$w\in L(H)$的分析树有一个同等大小的非常简单的类似于二叉树的结构。
　　为了使我们所讨论的这样的CFG和分析树更明确一点，将这样的行为称为定义上下文无关无法的乔姆斯基范式更为合适。

定义8.1. 一个上下文无关语法$G$是乔姆斯基范式仅当$G$的没条规都是如下三种形式之一：

1. 对于变量$X、\Upsilon、Z$，其中$\Upsilon、Z$都不是初始变量，有$X\rightarrow \Upsilon Z$。
2. 对于变量$X$和符号$a$，有$X\rightarrow a$。
3. 对于初始变量$S$，有$S\rightarrow \varepsilon$。

　　现在，乔姆斯基范式的CFG看起来很漂亮的原因是因为这个语法的每个分析树有一个简单的外形：变量节点形成了一个二叉树，每个变量节点都有两个变量孩子节点或者一个符号节点。有一个假想的例子用来表现我们所讨论的这种结构在图8.6中。注意初始变量只会在根节点出现一次，因为它被允许出现在任何规则的右边。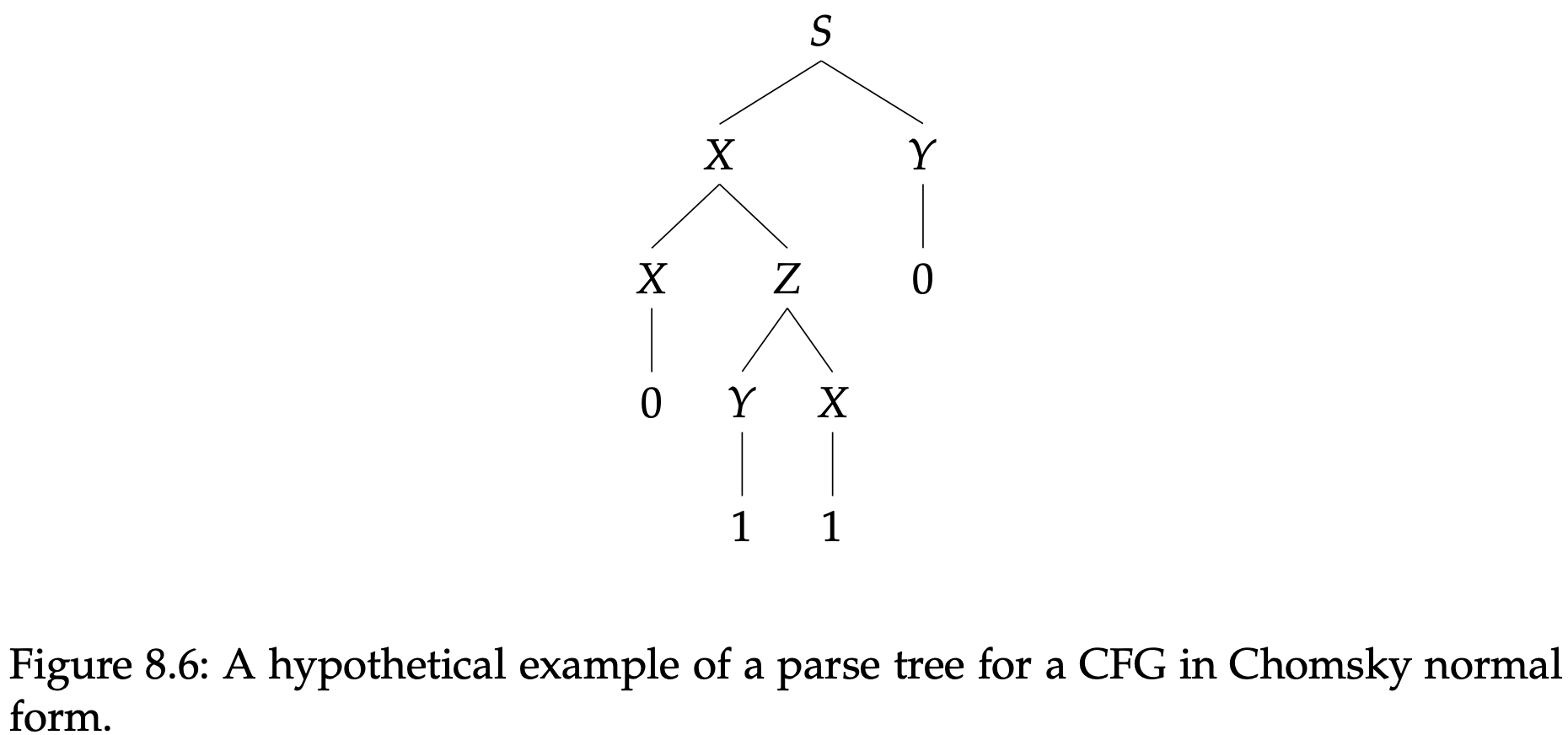

如果规则$S\rightarrow \varepsilon$出现在一个CFG的乔姆斯基范式中，那么我们就得到了一个不是上述结构的特殊情况。这种情况下，对于$\varepsilon$我们有一个非常简单的分析树如图8.7所示，这是这个字符串的唯一可能的分析树。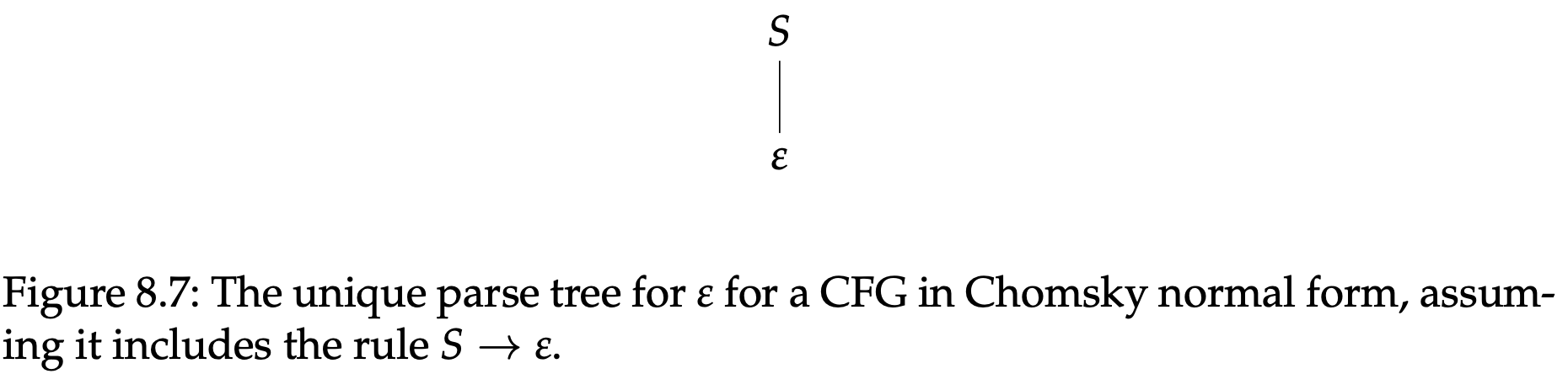

　　由于一个CFG $G$的乔姆斯基范式的分析树采用了特殊形式，每个已知字符串$w\in L(G)$的分析树一定恰好有$2|w|-1$个变量节点和$|w|$个叶子节点（除了特殊情况$w=\varepsilon$，只有一个变量节点和一个叶子节点）。一个等价的陈述是每个（非空）字符串$w$的乔姆斯基范式推导要求恰好$2|w|-1$次替换。
　　接下来这个定理确立了每个上下文无关语言都由一个乔姆斯基范式的CFG生成。

定理8.2. 已知$\Sigma$是一个字母表，$A\subseteq \Sigma^{*}$是一个上下文无关语言。存在一个乔姆斯基范式CFG $G$使得$A=L(G)$。

证明这个定义通常的方式是构造一个转换，将任意CFG $G$转换成乔姆斯基范式CFG $H$使得$L(H)=L(G)$。实际上我们应该基于一个任意CFG $G=(V,\Sigma,R,S)$来说明转换步骤。为了详细说明具体的步骤，让我们用一个具体的CFG来讲，他生成了我们上节课的括号配对语言$BAL$：

$$S\rightarrow (S)S\ |\ \varepsilon\tag{8.14}$$

1. 增加一个新的初始变量$S_0$和规则$S_0\rightarrow S$。这样做可以保证初始变量$S_0$不会出现在任何规则的右边。CFG（8.14）应用这个步骤后变成 $$\begin{align}&S_0\rightarrow S \\ &S\rightarrow (S)S\ |\ \varepsilon\end{align}\tag{8.15}$$
2. 为每个符号$a\in\Sigma$引入一个新的变量$X_a$。首先包括一个新的规则$X_a\rightarrow a$。然后对于每个$a$出现在右边的规则，只有$a$出现在右边的情况除外，将每个$a$替换成$X_a$。继续我们的例子，CFG（8.15）就会成（我们使用$L$和$R$来表示$X_($和$X_)$） $$\begin{align}&S_0\rightarrow S \\ &S\rightarrow LSRS\ |\ \varepsilon \\ &L\rightarrow ( \\ &R\rightarrow )\end{align}\tag{8.16}$$
3. 拆分形如$X\rightarrow \Upsilon_1 \cdot\cdot\cdot\Upsilon_m$的规则，其中$m\geq 3$，直接加入辅助变量来实现。特别是，$X\rightarrow \Upsilon_1 \cdot\cdot\cdot\Upsilon_m$能够被拆分为 $$\begin{align}X&\rightarrow \Upsilon_1 Z_2 \\ Z_2&\rightarrow \Upsilon_2 Z_3 \\ &\vdots \\ Z_{m-2}&\rightarrow \Upsilon_{m-2} Z_{m-1} \\ Z_{m-1}&\rightarrow \Upsilon_{m-1} \Upsilon_m\end{align}\tag{8.17}$$ 注意对于每条规则我们必须分开使用辅助变量，这样才不会导致规则之间的相互作用 — 不要重用同样的辅助变量破坏这个性质。用这种方式转换CFG（8.16）后得到 $$\begin{align}S_0&\rightarrow S \\ S&\rightarrow LZ_2\ |\ \varepsilon \\ Z_2&\rightarrow SZ_3 \\ Z_3&\rightarrow RS \\ L&\rightarrow ( \\ R&\rightarrow )\end{align}\tag{8.18}$$
4. 消除形如$X\rightarrow \varepsilon$的$\varepsilon$-规则，然后“修复这个损坏”。除了特殊情况$S_0\rightarrow \varepsilon$以外，其他地方不需要形如$X\rightarrow \varepsilon$的规则；通过简单地重复$X$出现在右边的规则，然后直接将每一种可能关联下的$X$替换成$\varepsilon$，我们就能到达同样的效果。你也许会通过这种方式引入新的$\varepsilon$-规则，但是他们能够被循环处理掉 — 任何一个新的$\varepsilon$-规则生成后就已经被消除掉了，并且不会被加回去。像这样转换CFG（8.18）后得到 $$\begin{align}S_0&\rightarrow S\ |\ \varepsilon \\ S&\rightarrow LZ_2 \\ Z_2&\rightarrow SZ_3\ |\ Z_3 \\ Z_3&\rightarrow RS\ |\ R \\ L&\rightarrow ( \\ R&\rightarrow )\end{align}\tag{8.18}$$ 注意我们最后得到的$\varepsilon$-规则是$S_0\rightarrow \varepsilon$，但是我们不会消除这个，因为$S_0\rightarrow \varepsilon$是被允许存在的$\varepsilon$-规则。
5. 消除单元规则，形式就像$X\rightarrow \Upsilon$。像这样的规则是没必要的，当我们发现规则$\Upsilon\rightarrow w$后就可以直接替换成$X\rightarrow w$。当你消除获得新规则以后，它就不会被加回去了。用这种方式转换CFG（8.19）得到 $$\begin{align}S_0&\rightarrow S\ |\ \varepsilon \\ S&\rightarrow LZ_2 \\ Z_2&\rightarrow SZ_3\ |\ RS\ |\ ) \\ Z_3&\rightarrow RS\ |\ ) \\ L&\rightarrow ( \\ R&\rightarrow )\end{align}\tag{8.18}$$ 到此我们就结束了；这个上下文无关语法就是一个乔姆斯基范式了。

上面这段藐视只是给出了你一个如何转换乔姆斯基范式的基本思路，并没有构造定理8.2的正式证明。然后如果更为正式和清楚地描述这个转换就可以得到一个定理8.2的正式证明。
　　当我们在证明有关上下文无关语言的东西时会经常用到这个定理，有时候它很有帮助，我们总是可以假设一个已知的上下文无关语言是通过一个乔姆斯基范式CFG生成的。
　　最后，着重强调一下乔姆斯基范式没有关于歧义性相关的内容。一个乔姆斯基范式的CFG可能是有歧义也可能没有，正如任意CFG一样。

原文链接

https://cs.uwaterloo.ca/~watrous/ToC-notes/ToC-notes.08.pdf