前言
在本节课中我们将会讨论图灵机计算模型。Alan Turing(1912-1954)在1963年提出了这个模型,并且以他的名字命名。Alan Turing对于本课程的影响怎么说都不会夸张 — 理论计算机科学的发展实际就是从图灵的工作开始的,并且由于这个原因他时常被称作理论计算机科学之父。
知识点
丘奇-图灵论题(The Church-Tring thesis)
图灵机模型的本意是为通用计算提供一个简单的数学抽象。图灵机计算代表着完全通用计算模型的概念被称作丘奇-图灵论题。这里有一个关于这个论题的陈述,但是你要明白重要的是思路,而不是用词的准确性。
丘奇-图灵论题: 任何能以机械过程计算的函数都能被图灵机计算。
注意这不是一个能被证明或者反驳的数学性陈述。如果你想要尝试证明这个陈述,首先你要做的是找到表示函数中“以机械过程计算”的数学定义,而且这正是图灵机模型打算提供的。
也有一些另外的计算模型可以为通用计算提供抽象。其中之一就是$\lambda$-微积分,它由Alonzo Church提出,并且在时间上还要早于图灵机的引进。这两种模型,图灵机和$\lambda$-微积分,从某种意义上来讲是等价的,任意计算能在其中一个中执行,也就能在另一个中执行。图灵在1936年的一篇文章上对此作了简要证明。我们将会在第14节课中还会讲到另一个例子,它叫堆栈机模型,和图灵机模型等价。基于堆栈机模型,或者直接使用图灵机模型,从概念上来说,想象一个抽象了随机存取机概念的计算模型的模仿并不困难。
虽然图灵机这样的机器现在已经有了,但是再现这个过程则纯属娱乐。图灵机模型意图不是充当一个执行计算的实际方法,而非要说的话,它的意图是为计算推理提供一个严格的数学根据 — 而且它被引进后,一直都做的很好。
图灵机模型的定义
在给出图灵机的正式定义前,我们先来看看通俗的描述。图灵机的构成有三个部分:
- 有限状态控制器。这个组件要求在每个瞬间图灵机处于有限状态中的一个。
- 磁带。这个组件由无限数量的磁带区块构成,每个区块在每个瞬间能存储有限磁带符号中的一个。并且磁带的左右都是无限长度的。
- 磁头。磁头可以在磁带上往左往右移动,这个可以理解为在每个计算步骤开始时正好能扫描一个磁带区块。磁头可以读取他所扫描区块中的符号,而且还能往这个区块写入一个新的符号。
图12.1阐述了这个三个组成部分。很自然能想到磁头用某种方式连接着有限状态控制器。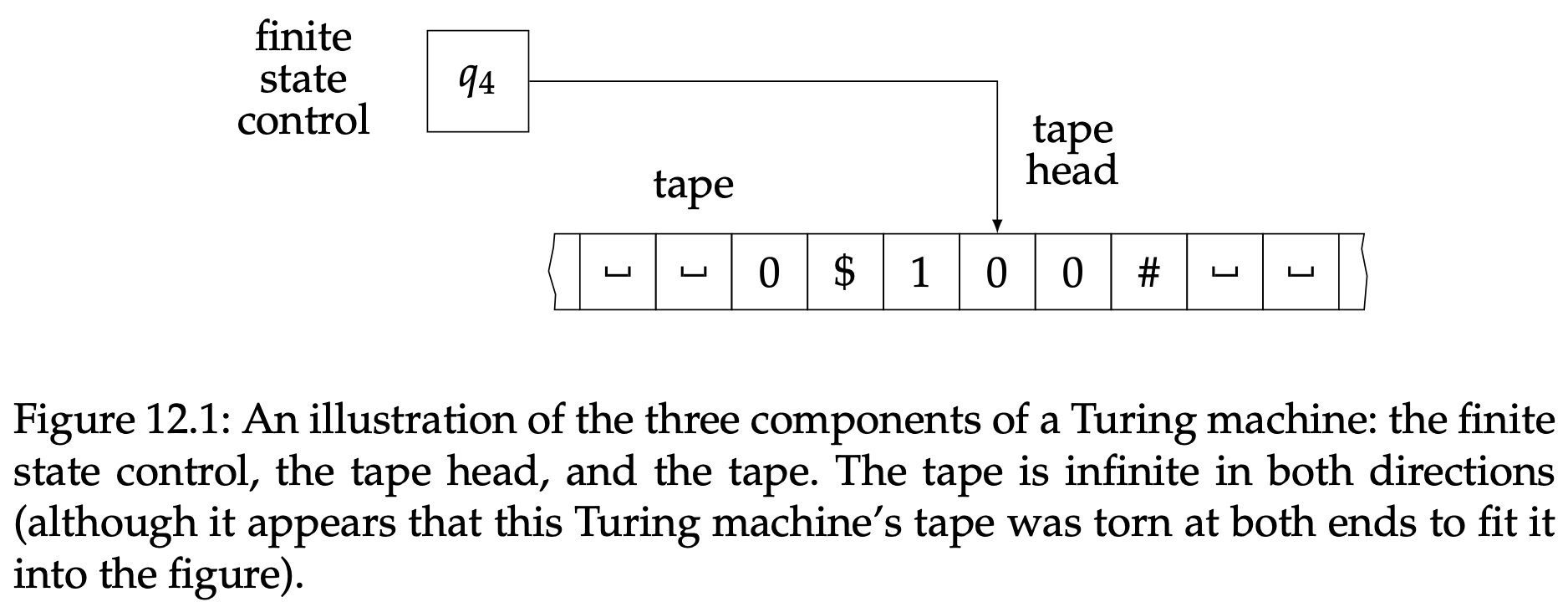
这个设计的思路是这样的,图灵机在每个瞬间的动作由有限状态控制器和当且磁头读取的磁带区块中的符号决定。这样,它的动作由优先数量的选择来决定:每个状态-符号对都对应着一个动作。取决于状态和被读取的符号,图灵机的动作可能包含改变有限状态控制器的状态,改变被扫面磁带区块的符号,向左或者向右移动磁头。一旦执行了动作,图灵机会更新有限状态控制器的状态,从磁带上读取某个符号,然后进程继续。你们可能会想到图灵机模型的确定性或者非确定性版本,但是我们的重点将放在在确定性版本的模型。
当一个图灵机开始一个计算,将输入字符串写在磁带上,其他的磁带区块初始化为空格符号,输入字符表中可能没有空格。我们需要一个可见的符号来表示空格,这里我们就用$\sqcup$来表示吧。一般来说,我们允许在磁带上写入可行的不包含在输入中的符号,也可以写入空格符号,因为有时候这样做会比较方便。
我们也会让图灵机可以终止计算进程并且返回一个输出,但这要求图灵机进入两种特殊状态:一个是接受状态$q_{acc}$和一个拒绝状态$q_{rej}$。这两个状态被视为停止状态,所有其他的状态都是非停止状态。如果一个图灵机进入了停止状态,会立刻停止计算,相应地接受或者拒绝。当我们讨论语言识别时,我们的关注点自然而然是在图灵机最后能否到达$q_{acc}$或者$q_{rej}$的中的一个状态,但是我们也能使用图灵机模型描述函数的计算,通过观察磁带上的内容怎么读取,什么时候到达停止状态。
DTM的正式定义
在看完以上图灵机的非正式表述后,我们接下来要进行正式定义了。
定义12.1. 一个确定性图灵机(或者简称DTM)是一个7-元组
其中$Q$是一个有限非空的状态集合,$\Sigma$是一个输入字母表,其中可能不包含空格符号$\sqcup$,$\Gamma$是一个磁带字母表,它满足$\Sigma\cup\{\sqcup\}\subseteq\Gamma$,$\delta$是一个转移函数,形式为
其中$q_0\in Q$是初始状态,$q_{acc}、q_{rej}\in Q$是接受和拒绝状态,它们必须满足$q_{acc}\neq q_{rej}$。
转移函数的解释如下。假设DTM现在的状态是$p\in Q$,磁头正从磁带上读取的符号是$a\in\Gamma$,然后情况是这样的
其中$D\in\{\leftarrow,\rightarrow\}$。DTM将要执行的动作是
- 将状态改变为$q$,
- 重写被磁头读取的磁带区块的内容为$b$,然后
- 按照$D$(向左或者向右)的方向移动磁头。
当处于状态$q_{acc}$或者$q_{rej}$时,转移函数没有指定动作,因为我们假设DTM在到达这两种状态时就立刻停止了。
图灵机计算
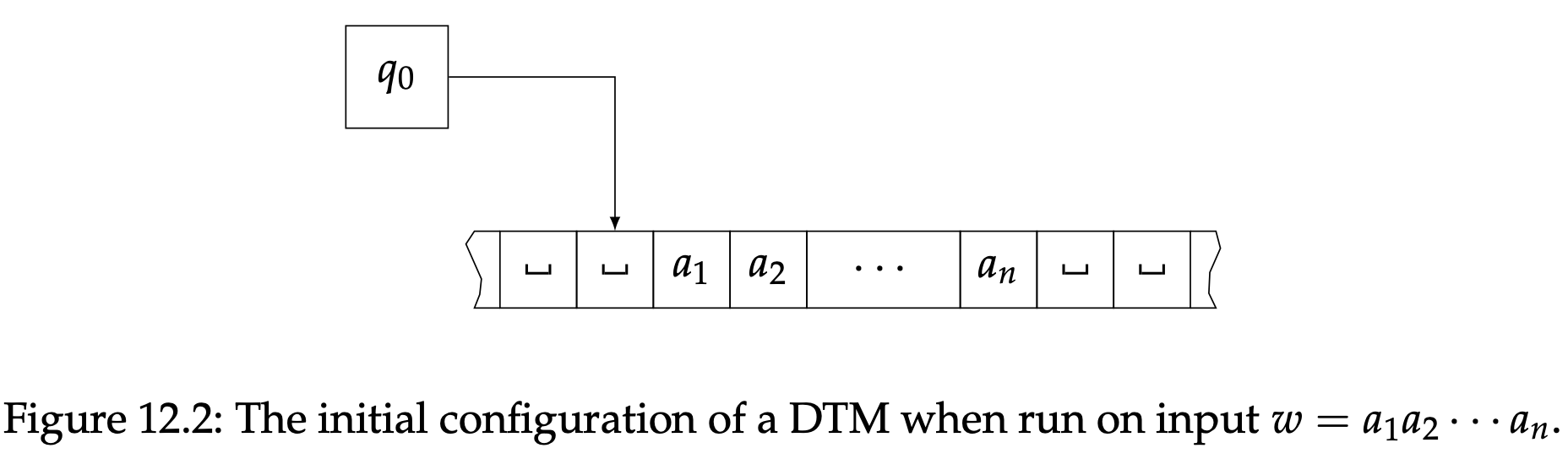
如果我们有一个DTM $M=(Q,\Sigma,\Gamma,\delta,q_0,q_{acc},q_{rej})$,我们想要思考对于某个输入字符串$w\in\Sigma^{*}$它的具体操作,我们假设它各个部分的初始化如图12.2所示.也就是,输入字符串在了磁带上,每个符号占据一个区块,其他的磁带区块写入空格符号,磁头的位置正好在左侧最靠近输入符号的一个空格符号上。如果输入字符串是$\varepsilon$,那么磁带上每个区块都是空格符号。
一旦DTM的初始化完成后,DTM就开始运行了,由上面提到的转移函数来确定具体动作。只要DTM不进入状态$q_{acc}$或者$q_{rej}$,计算就会继续进行。如果DTM最终进入了状态$q_{acc}$,那么它接受了输入字符串,而如果DTM最终进入了状态$q_{rej}$,那么它拒绝了输入字符串。这样,DTM面对输入字符串$w$有三种选择:
- $M$接受字符串$w$。
- $M$拒绝字符串$w$。
- $M$在输入$w$上一直运行。
在某些情况下我们可以设计一个特殊的DTM,它能避免第三种选择的发生,但普遍来说这是有可能的。
表达DTM的配置
为了更详细地说明图灵机以及声明关于它们行为的正式定义,我们需要多了解一些术语。当我们说道一个DTM的配置时,我们是在对图灵机在某一瞬间各个部分进行描述。这包括
- 有限状态控制器的状态,
- 整条磁带的内容,以及
- 磁头在磁带上的位置。
我们不是要像12.2那样画图来描绘图灵机的不同部分,而是要使用如下简短的概念来表达配置。如果我们有一个DTM $M=(Q,\Sigma,\Gamma,\delta,q_0,q_{acc},q_{rej})$,我们想要指代这个DTM的配置,我们的表达形式如下
其中状态$q\in Q$,符号$a\in\Gamma$,$u$和$v$是磁带上符号组成的字符串,并且
用文字表达就是,$u$和$v$都是磁带上字符构成的字符串,$u$不以空格开头,$v$不以空格结尾。表达式(12.4)的解释是它指代磁带上连续的字符串$uav$,而其他的磁带区块都是空格,并且$M$的状态是$q$,磁头正好在符号$a$的上方。比如,图12.1中DTM的配置表示为(因为美元符号是特殊符号,我用就用S来代替了)
而图12.2中DTM的配置则是
其中$w=a_1\cdots a_n$。
当你在对配置进行描述时,定义一些函数来辅助会非常方便。我们递归定义$\alpha:\Gamma^{*}\rightarrow\Gamma^{*}\setminus\{\cup\}\Gamma^{*}$和$\beta:\Gamma^{*}\rightarrow\Gamma^{*}\setminus\Gamma^{*}\{\sqcup\}$如下:
以及
然后我们将定义
改成
其中所有$u、v\in\Gamma^{*}$,$q\in Q$,$a\in\Gamma$。这并不像它看起来那么复杂:函数$\gamma$只是将$u$左边和$v$右边的空格全部丢掉,使得准确的表达式被保留。
DTM的产出映射
为了正式定义DTM的接受、拒绝、函数计算等含义,我们将会定义一个产出映射,类似于我们之前对上下文无关语法所做的。
定义12.2. 已知$M=(Q,\Sigma,\Gamma,\delta,q_0,q_{acc},q_{rej})$是一个DTM。产出映射$\vdash_M$是基于$M$成对的配置定义的,包含以下成对关系:
向右移动。对于每个状态$q\in Q\setminus\{q_{acc}、q_{rej}\},q\in Q$,以及符号$a、b\in \Gamma$满足
对于所有$u\in\Gamma^{*}\setminus\{\sqcup\}\Gamma^{*}、v\in\Gamma^{*}\setminus\Gamma^{*}\{\sqcup\}和c\in\Gamma$,产出映射包含的成对关系是:
向左移动。对于每个状态$p\in Q\setminus\{q_{acc},q_{rej}\}、q\in Q$,以及符号$a、b\in\Gamma$满足
对于所有$u\in\Gamma^{*}\setminus\{\sqcup\}\Gamma^{*}、v\in\Gamma^{*}\setminus\Gamma^{*}\{\sqcup\}和c\in\Gamma$,产出映射包含的成对关系是:
我们也使用$\vdash_M^{*}$表示$\vdash_M$的自反传递闭包。也就是,我们有
当且仅当存在整数$m\geq 1$,字符串$w_1,…,w_m,x_1,…,x_m\in\Gamma^{*}$,符号$c_1,…,c_m\in\Gamma$,状态$r_1,…,r_m\in Q$使得$u(p,a)v=w_1(r_1,c_1)x_1$,$y(q,b)v=w_m(r_m,c_m)x_m$以及对于所有$k\in\{1,…,m-1\}$满足
关于这些映射有一个更直观的描述为,表达式
表示$M$通过运行一个步骤将配置$u(p,a)v$转变成了配置$y(q,b)z$;而
表示$M$通过运行一定数量的步骤,可能为零,我们将会从配置$u(p,a)v$移动到配置$y(q,b)z$。
可判定和半可判定语言以及可计算函数
现在我们将会定义可判定和半可判定语言类以及可计算函数的概念。
为了定义可判定和半可判定语言类,我们需要用到上一个小节定义的产出映射来做正式表达,对于一个DTM接受和拒绝的含义是什么。
定义12.3. 已知$M=(Q,\Sigma,\Gamma,\delta,q_0,q_{acc},q_{rej})$是一个DTM,$w\in\Gamma^{*}$是一个字符串。如果存在字符串$u、v\in\Gamma^{*}$和符号$a\in\Gamma$使得
那么$M$接受$w$。如果存在字符串$u、v\in\Gamma^{*}$和符号$a\in\Gamma$使得
那么$M$拒绝$w$。如果这两个条件都不满足,那么$M$会在输入$w$上永远运行下去。
用文字表达就是,如果一个DTM被设置为对于某个输入字符串$w$的初始配置,然后开始运行,如果它最终进入接受状态,那么它就接受了$w$,如果它最终进入了拒绝状态,那么他就拒绝了$w$,但是要注意的是接受和拒绝状态是互相排斥的 — 因为DTM是确定性的,每个配置都有确定唯一的下一个配置,这就表示DTM $M$不可能同时接受又拒绝$w$。
类似于我们对其他计算模型所做的,我们用$L(M)$表示所有可以被DTM $M$接受的字符串所组成的语言。但是在DTM这种情况下,语言$L(M)$并没有告诉我们完整的信息 — 一个字符串$w\notin L(M)$是被拒绝了,还是它会造成$M$永远运行下去 — 但是不管怎样,这个概念是很有用的。
我们现在定义半可判定语言类就是那些能被某个DTM是被的语言。
定义12.4. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个语言。语言$A$是半可判定语言仅当存在一个DTM $M$使得$A=L(M)$。
半可判定这个名字可以反映出,假设存在$A=L(M)$,如果$w\in$,那么在$M$上输入$w$后运行,最终会通向接受状态;但是如果$w\notin A$,那么$M$可能会拒绝$w$,也可能会永远运行下去。也就是,$M$不能确定地告诉我们是否字符串$w$属于$A$,他只是“半可判定的”;对于如果$w\notin A$,你可能永远不会知道$M$对于$w$的确切结果。有一些可以用来替代可判定的命名,比如:图灵可识别,部分可判定,可递归枚举。
接下来,我们自然是要定义可判定语言,它的DTM可以正确告诉我们一个字符串是否属于它,并且不会永远运行下去。
定义12.5. 已知$\Sigma$是一个字母表,$A\subseteq\Sigma^{*}$是一个语言。语言$A$是可判定的仅当存在一个DTM $M$,它持有两种属性:
- $M$接受每个字符串$w\in A$。
- $M$拒绝每个字符串$w\notin A$。
有时候我们会用可递归和可计算来代替可判定这个名称。
最后,让我们来定义什么函数是可计算的。我们用函数将字符串映射为字符串,输入和输出的字母表不一定是相同的,这个普遍性在我们将来的课程中很重要。
定义12.6. 已知$\Sigma$和$\Gamma$是字母表,$f:\Sigma^{*}\rightarrow\Gamma^{*}$是一个函数。函数$f$是可计算的仅当存在一个DTM $M=(Q,\Sigma,\Delta,\delta,q_0,q_{acc},q_{rej})$使得映射
成立,其中每个字符串$w\in\Sigma^{*}$。这种情况我们也成DTM $M$计算了$f$。
在这个定义中,$\Delta$可能是任意磁带字母表;根据定义它必须包含所有输入字母表$\Sigma$中的符号,也必须包含字母表$\Gamma$中的所有符号,这些符号会出现在任意输出字符串中以满足(12.22)的映射关系。
用文字表达就是,一个函数可以通过一个DTM来计算仅当,在这个函数中运行的任意字符串时,它最终会接受,然后在磁带上留在由空格环绕的正确输出,并且磁头正好在这个输出字符串左边第一个区块。
一个图灵机的简单例子
现在我们来看一个简单的DTM例子,我们将会用状态图来描述它。在DTM的情况中,我们可以满足转移函数$\delta(p,a)=(q,b,\rightarrow)$的转移表示为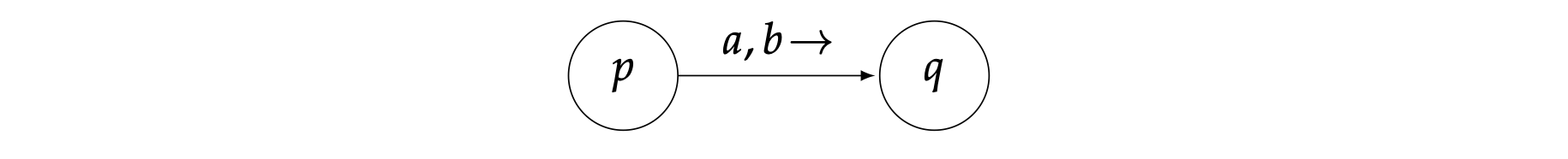
同样的满足$\delta(p,a)=(q,b,\leftarrow)$的转移表示为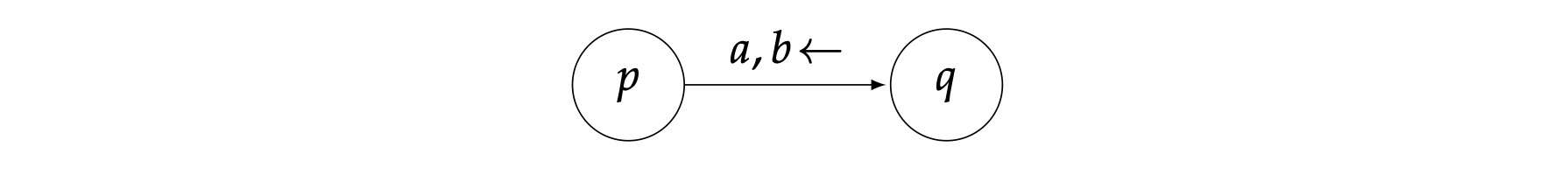
这个例子的状态图在下面图12.3中。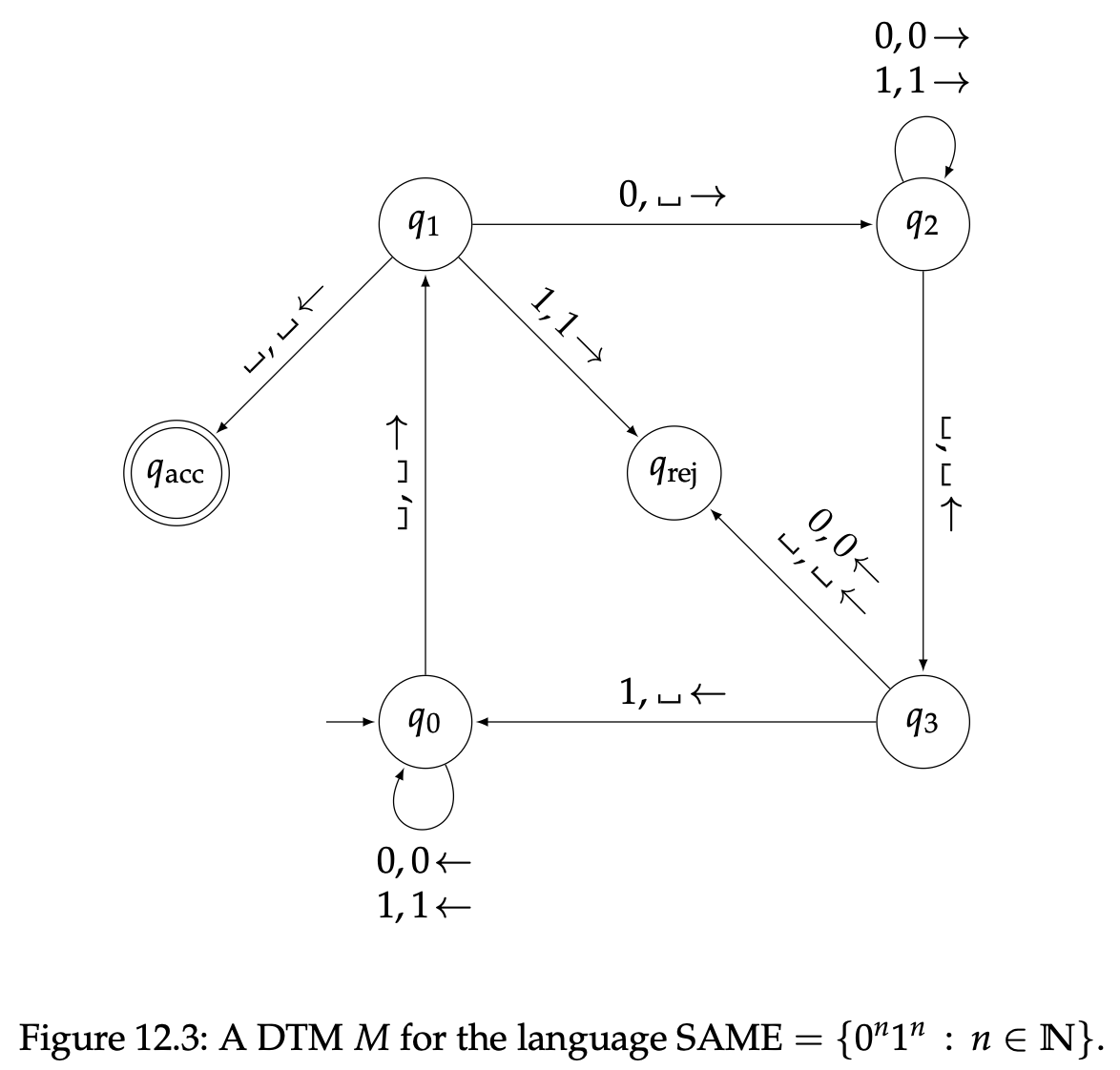
这个状态图中描述的DTM所识别的语言是
为了更明确一点,$M$接受每个字属于$SAME$的符串,并且拒绝每个输入$\overline{SAME}$的字符串,所以这个DTM不会永远运行下去。因此,$SAME$是可判定的。
DTM $M$运行的详细方式可以总结如下。DTM $M$刚开始正在扫描输入左侧的第一个空格。它向右移动磁头,如果它读入一个1就拒绝:因为这个输入的形式肯定不满足$0^n1^n$。另外,如果它读入另一个空格符号就接受:因为这个输入一定是一个空字符串,正好对应$SAME$中$n=0$的情况。否则,它一定会读入符号0,这个时候0会被擦除(替代的是一个空格符号),磁头重复向右移动,知道有一个空格出现,然后它会往回移动一个区块。如果这个区块中不是1,DTM就会拒绝:因为字符串的右边没有足够数量的1。相反,如果找到了一个1,将它擦除,磁头一路向左往回移动,然后我们对一个更短的字符串重复以上操作。
当然,这段概要只是用来启发,并没有告诉你具体DTM的运行 — 但是如果还没有12.3的状态图,这段概要也足够为你画出状态图提供思路了(可能画出来不太一样,但运行起来是类似的)。
事实上,有一个更高水平的概要可以描述DTM如何运作的基本思路。比如我们可以将DTM $M$的运行描述如下:
- 如果输入字符串是空串就接受。
- 确定最磁带上最左边的一个非空格符号是0,最右边的一个非空格符号是1。如果是情况属实,就擦除这两个符号回到第一步,否则就拒绝。
当然,有几种特定的方法可以用DTM来实现这个算法,图12.3中的DTM $M$就是其中一个。
我们现在所讨论的DTM $M$是相当简单的,当然他也不是典型的例子。能使我们感兴趣的DTM往往会更加复杂 — 事实上非常复杂,以致如果用状态图来表示它们会非常荒谬。真实情况下状态图是表现DTM几乎完全不会想用到的方法。如果用它来表示就等同于使用机械语言指令来编写复杂程序。
通常我们描述DTM的方式都是算法,通常表达的形式为伪代码或者高水平描述,就是上面最后一个关于$M$的描述。也许哪种高水平算法描述可以使用图灵机运行并不是十分明显,但是由直觉引导我们相信如果一个算法能用你所喜爱的编程语言编写,那么它也一定能在确定性图灵机上运行。接下来两节课的讨论主要是为了帮助建立这种直觉。